No CrossRef data available.
Published online by Cambridge University Press: 18 September 2023
Let 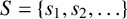 $S=\{s_{1}, s_{2}, \ldots \}$ be an unbounded sequence of positive integers with
$S=\{s_{1}, s_{2}, \ldots \}$ be an unbounded sequence of positive integers with 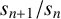 $s_{n+1}/s_{n}$ approaching
$s_{n+1}/s_{n}$ approaching 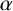 $\alpha $ as
$\alpha $ as 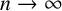 $n\rightarrow \infty $ and let
$n\rightarrow \infty $ and let 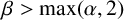 $\beta>\max (\alpha , 2)$. We show that for all sufficiently large positive integers l, if
$\beta>\max (\alpha , 2)$. We show that for all sufficiently large positive integers l, if 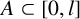 $A\subset [0, l]$ with
$A\subset [0, l]$ with 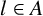 $l\in A$,
$l\in A$, 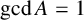 $\gcd A=1$ and
$\gcd A=1$ and 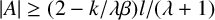 $|A|\geq (2-{k}/{\lambda \beta })l/(\lambda +1)$, where
$|A|\geq (2-{k}/{\lambda \beta })l/(\lambda +1)$, where 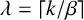 $\lambda =\lceil {k}/{\beta }\rceil $, then
$\lambda =\lceil {k}/{\beta }\rceil $, then 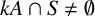 $kA\cap S\neq \emptyset $ for
$kA\cap S\neq \emptyset $ for 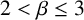 $2<\beta \leq 3$ and
$2<\beta \leq 3$ and 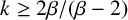 $k\geq {2\beta }/{(\beta -2)}$ or for
$k\geq {2\beta }/{(\beta -2)}$ or for 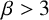 $\beta>3$ and
$\beta>3$ and 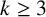 $k\geq 3$.
$k\geq 3$.
This work was supported by the National Natural Science Foundation of China (Grant Nos. 11071033, 12371003) and the Top Talents Project of Anhui Department of Education (Grant No. gxbjZD05).