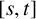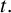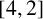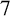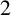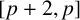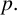1 Introduction
We consider finite simple graphs, and use standard terminology and notation from [Reference Bondy and Murty3, Reference West8]. The order of a graph is its number of vertices and the size is its number of edges. A k-cycle is a cycle of length
![]() $k.$
In 1971, Bondy [Reference Bondy1] introduced the concept of a pancyclic graph. A graph G of order n is called pancyclic if for every integer k with
$k.$
In 1971, Bondy [Reference Bondy1] introduced the concept of a pancyclic graph. A graph G of order n is called pancyclic if for every integer k with
![]() $3\le k\le n, G$
contains a k-cycle. For an account of these graphs, see [Reference George, Khodkar and Wallis5].
$3\le k\le n, G$
contains a k-cycle. For an account of these graphs, see [Reference George, Khodkar and Wallis5].
Definition 1.1. Let s and t be given integers. A graph G is called an
![]() $[s,t]$
-graph if any induced subgraph of G of order s has size at least
$[s,t]$
-graph if any induced subgraph of G of order s has size at least
![]() $t.$
$t.$
Denote by
![]() $\alpha (G)$
the independence number of a graph G. We note two facts:
$\alpha (G)$
the independence number of a graph G. We note two facts:
-
(1) every
 $[s,t]$
-graph is an
$[s,t]$
-graph is an
 $[s+1,t+1]$
-graph;
$[s+1,t+1]$
-graph; -
(2)
 $\alpha (G)\le k$
if and only if G is a
$\alpha (G)\le k$
if and only if G is a
 $[k+1,1]$
-graph.
$[k+1,1]$
-graph.
Thus, the concept of an
![]() $[s,t]$
-graph is an extension of the independence number. We are interested in two results about
$[s,t]$
-graph is an extension of the independence number. We are interested in two results about
![]() $[4,2]$
graphs.
$[4,2]$
graphs.
Theorem 1.2 (Liu and Wang, [Reference Liu and Wang6]).
Every
![]() $2$
-connected
$2$
-connected
![]() $[4,2]$
-graph of order at least
$[4,2]$
-graph of order at least
![]() $6$
is Hamiltonian.
$6$
is Hamiltonian.
Theorem 1.3 (Liu, Wang and Gao, [Reference Liu, Wang and Gao7]).
Let G be a
![]() $2$
-connected
$2$
-connected
![]() $[4,2]$
-graph of order n with
$[4,2]$
-graph of order n with
![]() $n\ge 7.$
If G contains a k-cycle with
$n\ge 7.$
If G contains a k-cycle with
![]() $k<n,$
then G contains a
$k<n,$
then G contains a
![]() $(k+1)$
-cycle.
$(k+1)$
-cycle.
We strengthen Theorem 1.3 by proving that every
![]() $2$
-connected
$2$
-connected
![]() $[4,2]$
-graph of order at least
$[4,2]$
-graph of order at least
![]() $7$
is pancyclic (Theorem 2.5). To do so, we will determine the triangle-free graphs among
$7$
is pancyclic (Theorem 2.5). To do so, we will determine the triangle-free graphs among
![]() $[p+2,p]$
-graphs. This preliminary result (Lemma 2.4) is of independent interest.
$[p+2,p]$
-graphs. This preliminary result (Lemma 2.4) is of independent interest.
2 Main results
We denote by
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
the vertex set and edge set of a graph
$E(G)$
the vertex set and edge set of a graph
![]() $G,$
respectively, and denote by
$G,$
respectively, and denote by
![]() $|G|$
and
$|G|$
and
![]() $e(G)$
the order and size of
$e(G)$
the order and size of
![]() $G,$
respectively. Thus,
$G,$
respectively. Thus,
![]() $|G|=|V(G)|$
and
$|G|=|V(G)|$
and
![]() $e(G)=|E(G)|.$
For a vertex subset
$e(G)=|E(G)|.$
For a vertex subset
![]() $S\subseteq V(G),$
we use
$S\subseteq V(G),$
we use
![]() $G[S]$
to denote the subgraph of G induced by
$G[S]$
to denote the subgraph of G induced by
![]() $S.$
The neighbourhood of a vertex x is denoted by
$S.$
The neighbourhood of a vertex x is denoted by
![]() $N(x)$
and the closed neighbourhood of x is
$N(x)$
and the closed neighbourhood of x is
![]() $N[x]\triangleq N(x)\cup \{x\}.$
The degree of x is denoted by
$N[x]\triangleq N(x)\cup \{x\}.$
The degree of x is denoted by
![]() $\textrm {deg}(x).$
For
$\textrm {deg}(x).$
For
![]() $S\subseteq V(G), N_S(x)\triangleq N(x)\cap S$
and the degree of x in S is
$S\subseteq V(G), N_S(x)\triangleq N(x)\cap S$
and the degree of x in S is
![]() $\textrm {deg}_S(x)\triangleq |N_S(x)|.$
Given two vertex subsets S and T of
$\textrm {deg}_S(x)\triangleq |N_S(x)|.$
Given two vertex subsets S and T of
![]() $G,$
we denote by
$G,$
we denote by
![]() $[S, T]$
the set of edges having one endpoint in S and the other in
$[S, T]$
the set of edges having one endpoint in S and the other in
![]() $T.$
The degree of S is
$T.$
The degree of S is
![]() $\textrm {deg}(S)\triangleq |[S, \overline {S}]|,$
where
$\textrm {deg}(S)\triangleq |[S, \overline {S}]|,$
where
![]() $\overline {S}=V(G)\setminus S.$
We denote by
$\overline {S}=V(G)\setminus S.$
We denote by
![]() $C_n$
and
$C_n$
and
![]() $K_n$
the cycle of order n and the complete graph of order
$K_n$
the cycle of order n and the complete graph of order
![]() $n,$
respectively. Finally,
$n,$
respectively. Finally,
![]() $\overline {G}$
denotes the complement of a graph
$\overline {G}$
denotes the complement of a graph
![]() $G.$
$G.$
We will need the following two lemmas on integral quadratic forms.
Lemma 2.1. Given positive integers
![]() $n\ge k\ge 2,$
let
$n\ge k\ge 2,$
let
![]() $x_1,x_2,\ldots ,x_k$
be positive integers such that
$x_1,x_2,\ldots ,x_k$
be positive integers such that
![]() $\sum _{i=1}^k x_i =n.$
Then,
$\sum _{i=1}^k x_i =n.$
Then,
 $$ \begin{align} n-1\le \sum_{i=1}^{k-1}x_ix_{i+1}\le\begin{cases}\lfloor n/2\rfloor\cdot \lceil n/2\rceil& \textrm{if}\,\,\,k=2,\,3,\\ ab+k-5 & \textrm{if}\,\,\,k\ge 4, \end{cases} \end{align} $$
$$ \begin{align} n-1\le \sum_{i=1}^{k-1}x_ix_{i+1}\le\begin{cases}\lfloor n/2\rfloor\cdot \lceil n/2\rceil& \textrm{if}\,\,\,k=2,\,3,\\ ab+k-5 & \textrm{if}\,\,\,k\ge 4, \end{cases} \end{align} $$
where
![]() $a=\lfloor (n-k+4)/2\rfloor $
and
$a=\lfloor (n-k+4)/2\rfloor $
and
![]() $b=\lceil (n-k+4)/2\rceil .$
For any n and
$b=\lceil (n-k+4)/2\rceil .$
For any n and
![]() $k,$
the lower and upper bounds in (2.1) can be attained.
$k,$
the lower and upper bounds in (2.1) can be attained.
Proof. Define a quadratic polynomial
![]() $f(x_1,x_2,\ldots ,x_k)=\sum _{i=1}^{k-1}x_ix_{i+1}.$
We first prove the left-hand inequality in (2.1). Let
$f(x_1,x_2,\ldots ,x_k)=\sum _{i=1}^{k-1}x_ix_{i+1}.$
We first prove the left-hand inequality in (2.1). Let
![]() $x_j={\min }\{x_i \,|\, 1\le i\le k\}.$
We have
$x_j={\min }\{x_i \,|\, 1\le i\le k\}.$
We have
 $$ \begin{align*} f(x_1,x_2,\ldots,x_k)&\ge x_1x_j+\cdots+x_{j-1}x_j+x_jx_{j+1}+x_jx_{j+2}+\cdots+x_jx_k\\ &=x_j(x_1+\cdots+x_{j-1}+x_{j+1}+\cdots+x_k)\\ &=x_j(n-x_j)\\ &\ge n-1. \end{align*} $$
$$ \begin{align*} f(x_1,x_2,\ldots,x_k)&\ge x_1x_j+\cdots+x_{j-1}x_j+x_jx_{j+1}+x_jx_{j+2}+\cdots+x_jx_k\\ &=x_j(x_1+\cdots+x_{j-1}+x_{j+1}+\cdots+x_k)\\ &=x_j(n-x_j)\\ &\ge n-1. \end{align*} $$
This proves the first inequality in (2.1). The lower bound
![]() $n-1$
is attained for
$n-1$
is attained for
![]() $x_1=n-k+1, x_2=\cdots =x_k=1.$
$x_1=n-k+1, x_2=\cdots =x_k=1.$
Now we prove the second inequality in (2.1). The case
![]() $k=2$
is an elementary fact:
$k=2$
is an elementary fact:
![]() $f(x_1,x_2)=x_1 x_2\le \lfloor n/2\rfloor \cdot \lceil n/2\rceil $
, where equality holds when
$f(x_1,x_2)=x_1 x_2\le \lfloor n/2\rfloor \cdot \lceil n/2\rceil $
, where equality holds when
![]() $x_1=\lfloor n/2\rfloor $
and
$x_1=\lfloor n/2\rfloor $
and
![]() $x_2=\lceil n/2\rceil .$
The case
$x_2=\lceil n/2\rceil .$
The case
![]() $k=3$
reduces to the case
$k=3$
reduces to the case
![]() $k=2$
as follows:
$k=2$
as follows:
where equality holds when
![]() $x_2=\lfloor n/2\rfloor $
and
$x_2=\lfloor n/2\rfloor $
and
![]() $x_1+x_3=\lceil n/2\rceil .$
Next, suppose
$x_1+x_3=\lceil n/2\rceil .$
Next, suppose
![]() $k\ge 4.$
Denote by
$k\ge 4.$
Denote by
![]() $f_{\max }$
the maximum value of
$f_{\max }$
the maximum value of
![]() $f.$
If
$f.$
If
![]() $x_1{\kern-1pt}>{\kern-1pt}1,$
with
$x_1{\kern-1pt}>{\kern-1pt}1,$
with
![]() $x_1^{\prime }{\kern-1pt}={\kern-1pt}1, x_2^{\prime }{\kern-1pt}={\kern-1pt}x_2, x_3^{\prime }{\kern-1pt}={\kern-1pt}x_3{\kern-1pt}+{\kern-1pt}x_1{\kern-1pt}-{\kern-1pt}1$
and
$x_1^{\prime }{\kern-1pt}={\kern-1pt}1, x_2^{\prime }{\kern-1pt}={\kern-1pt}x_2, x_3^{\prime }{\kern-1pt}={\kern-1pt}x_3{\kern-1pt}+{\kern-1pt}x_1{\kern-1pt}-{\kern-1pt}1$
and
![]() $x_i^{\prime }=x_i$
for
$x_i^{\prime }=x_i$
for
![]() $i\ge 4$
, then
$i\ge 4$
, then
Similarly analysing the variable
![]() $x_k,$
we deduce that
$x_k,$
we deduce that
![]() $f_{\max }$
can only be attained at some
$f_{\max }$
can only be attained at some
![]() $x_1,\ldots ,x_k$
when
$x_1,\ldots ,x_k$
when
![]() $x_1=x_k=1,$
which we now assume. With
$x_1=x_k=1,$
which we now assume. With
![]() $x_2^{\prime }=1, x_3^{\prime }=x_3, x_4^{\prime }=x_4+x_2-1$
and
$x_2^{\prime }=1, x_3^{\prime }=x_3, x_4^{\prime }=x_4+x_2-1$
and
![]() $x_i^{\prime }=x_i$
for
$x_i^{\prime }=x_i$
for
![]() $i=5,\ldots ,k-1$
,
$i=5,\ldots ,k-1$
,
Hence,
![]() $f_{\max }$
can be attained at a certain
$f_{\max }$
can be attained at a certain
![]() $(1,1,x_3,\ldots ,x_{k-1},1).$
Successively applying this argument, we deduce that
$(1,1,x_3,\ldots ,x_{k-1},1).$
Successively applying this argument, we deduce that
![]() $f_{\max }$
can be attained at
$f_{\max }$
can be attained at
![]() $(1,1,\ldots ,1,x_{k-2},x_{k-1},1).$
Now
$(1,1,\ldots ,1,x_{k-2},x_{k-1},1).$
Now
![]() $(x_{k-2}+1)+(x_{k-1}+1)=n-k+4$
and so
$(x_{k-2}+1)+(x_{k-1}+1)=n-k+4$
and so
 $$ \begin{align*} f(1,1,\ldots,1,x_{k-2},x_{k-1},1)&=(x_{k-2}+1)(x_{k-1}+1)+k-5\\ &\le \lfloor (n-k+4)/2\rfloor\cdot \lceil (n-k+4)/2\rceil+k-5. \end{align*} $$
$$ \begin{align*} f(1,1,\ldots,1,x_{k-2},x_{k-1},1)&=(x_{k-2}+1)(x_{k-1}+1)+k-5\\ &\le \lfloor (n-k+4)/2\rfloor\cdot \lceil (n-k+4)/2\rceil+k-5. \end{align*} $$
This proves the second inequality in (2.1). The upper bound is attained at
![]() $x_1=x_2=\cdots =x_{k-3}=x_k=1, x_{k-2}=\lfloor (n-k+2)/2\rfloor $
and
$x_1=x_2=\cdots =x_{k-3}=x_k=1, x_{k-2}=\lfloor (n-k+2)/2\rfloor $
and
![]() $x_{k-1}=\lceil (n-k+2)/2\rceil .$
$x_{k-1}=\lceil (n-k+2)/2\rceil .$
Lemma 2.2 [Reference Zhan9, Theorem 1].
Given positive integers
![]() $n\ge k\ge 2,$
let
$n\ge k\ge 2,$
let
![]() $x_1,x_2,\ldots ,x_k$
be positive integers such that
$x_1,x_2,\ldots ,x_k$
be positive integers such that
![]() $\sum _{i=1}^k x_i =n.$
Then,
$\sum _{i=1}^k x_i =n.$
Then,
 $$ \begin{align} 2n-k\le \sum_{i=1}^k x_ix_{i+1}, \end{align} $$
$$ \begin{align} 2n-k\le \sum_{i=1}^k x_ix_{i+1}, \end{align} $$
where
![]() $x_{k+1}\triangleq x_1.$
For any n and
$x_{k+1}\triangleq x_1.$
For any n and
![]() $k,$
the lower bound in (2.2) can be attained.
$k,$
the lower bound in (2.2) can be attained.
A sharp upper bound on the quadratic form in (2.2) is also determined in [Reference Zhan9], but we do not need it here.
Definition 2.3. Given a graph H and a positive integer
![]() $k,$
the k-blow-up of
$k,$
the k-blow-up of
![]() $H,$
denoted by
$H,$
denoted by
![]() $H^{(k)},$
is the graph obtained by replacing every vertex of H with k different vertices where a copy of u is adjacent to a copy of v in the blow-up graph if and only if u is adjacent to v in
$H^{(k)},$
is the graph obtained by replacing every vertex of H with k different vertices where a copy of u is adjacent to a copy of v in the blow-up graph if and only if u is adjacent to v in
![]() $H.$
$H.$
For example,
![]() $C_5^{(2)}$
is depicted in Figure 1.
$C_5^{(2)}$
is depicted in Figure 1.

Figure 1 The 2-blow-up of
![]() $C_5$
.
$C_5$
.
Now we are ready to determine the triangle-free graphs among
![]() $[p+2,p]$
-graphs. For a graph G, we denote by
$[p+2,p]$
-graphs. For a graph G, we denote by
![]() $\delta (G)$
and
$\delta (G)$
and
![]() $\Delta (G)$
its minimum and maximum degrees, respectively. We regard isomorphic graphs as the same graph. Thus, for two graphs G and
$\Delta (G)$
its minimum and maximum degrees, respectively. We regard isomorphic graphs as the same graph. Thus, for two graphs G and
![]() $H,$
the notation
$H,$
the notation
![]() $G=H$
means that G and H are isomorphic.
$G=H$
means that G and H are isomorphic.
Lemma 2.4. Let G be a
![]() $[p+2,p]$
-graph of order n with
$[p+2,p]$
-graph of order n with
![]() $\delta (G)\ge p\ge 2$
and
$\delta (G)\ge p\ge 2$
and
![]() $n\ge 2p+3.$
Then, G is triangle-free if and only if p is even,
$n\ge 2p+3.$
Then, G is triangle-free if and only if p is even,
![]() $p\ge 6$
and
$p\ge 6$
and
![]() $G=C_5^{(p/2)}.$
$G=C_5^{(p/2)}.$
Proof. We will repeatedly use the condition that G is a
![]() $[p+2,p]$
-graph without necessarily mentioning it. Denote
$[p+2,p]$
-graph without necessarily mentioning it. Denote
![]() $\Delta =\Delta (G)$
and choose a vertex
$\Delta =\Delta (G)$
and choose a vertex
![]() $x\in V(G)$
such that
$x\in V(G)$
such that
![]() $\textrm {deg}(x)=\Delta .$
Let
$\textrm {deg}(x)=\Delta .$
Let
![]() $S=N(x)$
and
$S=N(x)$
and
![]() $T=V(G)\setminus S.$
Then,
$T=V(G)\setminus S.$
Then,
![]() $|S|=\Delta .$
$|S|=\Delta .$
Suppose that G is triangle-free. Then, S is an independent set. Since G is a
![]() $[p+2,p]$
-graph,
$[p+2,p]$
-graph,
![]() $\Delta \le p+1.$
We assert that
$\Delta \le p+1.$
We assert that
![]() $\Delta =p$
and hence G is p-regular, since
$\Delta =p$
and hence G is p-regular, since
![]() $\delta (G)\ge p$
by the assumption. Otherwise,
$\delta (G)\ge p$
by the assumption. Otherwise,
![]() $\Delta =p+1.$
Since
$\Delta =p+1.$
Since
![]() $n\ge 2p+3,\ |T|\ge p+2.$
Thus,
$n\ge 2p+3,\ |T|\ge p+2.$
Thus,
![]() $G[T]$
contains an edge
$G[T]$
contains an edge
![]() $uv$
and
$uv$
and
![]() $|\{u\}\cup S|=p+2$
implies that
$|\{u\}\cup S|=p+2$
implies that
![]() $\textrm {deg}_S(u)\ge p.$
Similarly,
$\textrm {deg}_S(u)\ge p.$
Similarly,
![]() $\textrm {deg}_S(v)\ge p.$
Since
$\textrm {deg}_S(v)\ge p.$
Since
![]() $p+p=2p>p+1=|S|,$
we have
$p+p=2p>p+1=|S|,$
we have
![]() $N_S(u)\cap N_S(v)\neq \emptyset .$
Let
$N_S(u)\cap N_S(v)\neq \emptyset .$
Let
![]() $w\in N_S(u)\cap N_S(v).$
Then,
$w\in N_S(u)\cap N_S(v).$
Then,
![]() $wuvw$
is a triangle, which is a contradiction. This shows that G is p-regular.
$wuvw$
is a triangle, which is a contradiction. This shows that G is p-regular.
Let
![]() $y\in S$
and denote
$y\in S$
and denote
![]() $C=N(y).$
Then, C is an independent set and
$C=N(y).$
Then, C is an independent set and
![]() $|C|=p.$
Denote
$|C|=p.$
Denote
![]() $D=T\setminus C.$
The structure of G is illustrated in Figure 2.
$D=T\setminus C.$
The structure of G is illustrated in Figure 2.

Figure 2 The structure of G.
Since
![]() $n\ge 2p+3,$
we have
$n\ge 2p+3,$
we have
![]() $|D|=n-2p\ge 3.$
Thus, D is not a clique, since G is triangle-free. Let z and f be any two distinct nonadjacent vertices in
$|D|=n-2p\ge 3.$
Thus, D is not a clique, since G is triangle-free. Let z and f be any two distinct nonadjacent vertices in
![]() $D.$
Since
$D.$
Since
![]() $|\{z,f\}\cup S|=p+2, |\{z,f\}\cup C|=p+2$
, and S and C are independent sets,
$|\{z,f\}\cup S|=p+2, |\{z,f\}\cup C|=p+2$
, and S and C are independent sets,
Note that
![]() $S\cap C=\emptyset $
and
$S\cap C=\emptyset $
and
![]() $\textrm {deg}(z)=\textrm {deg}(f)=p.$
We must have
$\textrm {deg}(z)=\textrm {deg}(f)=p.$
We must have
We assert that D is an independent set. Otherwise, D contains two adjacent vertices
![]() $u_1$
and
$u_1$
and
![]() $u_2.$
Let
$u_2.$
Let
![]() $u_3\in D\setminus \{u_1, u_2\}.$
Since G is triangle-free,
$u_3\in D\setminus \{u_1, u_2\}.$
Since G is triangle-free,
![]() $u_3$
is nonadjacent to at least one vertex in
$u_3$
is nonadjacent to at least one vertex in
![]() $\{u_1, u_2\},$
say,
$\{u_1, u_2\},$
say,
![]() $u_1$
. Setting
$u_1$
. Setting
![]() $z=u_1$
and
$z=u_1$
and
![]() $f=u_3$
in (2.3), we deduce that
$f=u_3$
in (2.3), we deduce that
![]() $|[\{u_1,u_3\}, S\cup C]|=2p.$
However, since both
$|[\{u_1,u_3\}, S\cup C]|=2p.$
However, since both
![]() $u_1$
and
$u_1$
and
![]() $u_3$
have degree
$u_3$
have degree
![]() $p,$
and
$p,$
and
![]() $u_1$
already has a neighbour
$u_1$
already has a neighbour
![]() $u_2\not \in S\cup C,$
we have
$u_2\not \in S\cup C,$
we have
![]() $|[\{u_1,u_3\}, S\cup C]|\le 2p-1,$
which is a contradiction.
$|[\{u_1,u_3\}, S\cup C]|\le 2p-1,$
which is a contradiction.
Observe that now (2.3) holds for any two distinct vertices z and f in
![]() $D.$
Equation (2.3) has the equivalent form
$D.$
Equation (2.3) has the equivalent form
Then, (2.4) and
![]() $|D|\ge 3$
imply that for any vertex
$|D|\ge 3$
imply that for any vertex
![]() $z\in D,$
$z\in D,$
To see this, in contrast, first suppose
![]() $\textrm {deg}_S(z)>p/2.$
Then, by the first equality in (2.4), for any two other vertices
$\textrm {deg}_S(z)>p/2.$
Then, by the first equality in (2.4), for any two other vertices
![]() $f,r\in D$
, we have
$f,r\in D$
, we have
![]() $\textrm {deg}_S(f)<p/2$
and
$\textrm {deg}_S(f)<p/2$
and
![]() $\textrm {deg}_S(r)<p/2,$
yielding
$\textrm {deg}_S(r)<p/2,$
yielding
![]() $\textrm {deg}_S(f)+\textrm {deg}_S(r)<p,$
which contradicts (2.4). If
$\textrm {deg}_S(f)+\textrm {deg}_S(r)<p,$
which contradicts (2.4). If
![]() $\textrm {deg}_S(z)<p/2,$
the same argument gives a contradiction. A similar analysis with C in place of S shows
$\textrm {deg}_S(z)<p/2,$
the same argument gives a contradiction. A similar analysis with C in place of S shows
![]() $\textrm {deg}_C(z)=p/2.$
Thus, we have proved (2.5). In particular,
$\textrm {deg}_C(z)=p/2.$
Thus, we have proved (2.5). In particular,
![]() $q\triangleq p/2$
is a positive integer, that is, p is even. Now choose an arbitrary but fixed vertex
$q\triangleq p/2$
is a positive integer, that is, p is even. Now choose an arbitrary but fixed vertex
![]() $t\in D$
and denote
$t\in D$
and denote
![]() $B=N_S(t), C_2=N_C(t), A=S\setminus B$
and
$B=N_S(t), C_2=N_C(t), A=S\setminus B$
and
![]() $C_1=C\setminus C_2$
(see the illustration in Figure 2). We have
$C_1=C\setminus C_2$
(see the illustration in Figure 2). We have
Since G is p-regular of order
![]() $n\ge 2p+3,$
it is impossible that
$n\ge 2p+3,$
it is impossible that
![]() $p=2.$
Otherwise, G would be a
$p=2.$
Otherwise, G would be a
![]() $2$
-regular graph of order
$2$
-regular graph of order
![]() $\ge 7,$
which is not a
$\ge 7,$
which is not a
![]() $[4,2]$
-graph. Thus,
$[4,2]$
-graph. Thus,
![]() $p\ge 4$
and
$p\ge 4$
and
![]() $q\ge 2.$
$q\ge 2.$
Choose any two distinct vertices
![]() $v_1, v_2\in C_2.$
Then,
$v_1, v_2\in C_2.$
Then,
![]() $|\{v_1, v_2\}\cup S|=p+2$
implies that
$|\{v_1, v_2\}\cup S|=p+2$
implies that
![]() $|[\{v_1, v_2\}, S]|\ge p.$
Since G is triangle-free,
$|[\{v_1, v_2\}, S]|\ge p.$
Since G is triangle-free,
![]() $N(v_i)\cap B=\emptyset $
for
$N(v_i)\cap B=\emptyset $
for
![]() $i=1, 2.$
Hence,
$i=1, 2.$
Hence,
![]() $N_S(v_i)=N_A(v_i)$
for
$N_S(v_i)=N_A(v_i)$
for
![]() $i=1, 2.$
However,
$i=1, 2.$
However,
![]() $|A|=q.$
We have
$|A|=q.$
We have
![]() $N_S(v_i)=A$
and
$N_S(v_i)=A$
and
![]() $\textrm {deg}_A(v_i)=q$
for
$\textrm {deg}_A(v_i)=q$
for
![]() $i=1,2,$
implying that every vertex in
$i=1,2,$
implying that every vertex in
![]() $C_2$
is adjacent to every vertex in
$C_2$
is adjacent to every vertex in
![]() $A.$
$A.$
Choose any two distinct vertices
![]() $v_3, v_4\in C_1.$
Then,
$v_3, v_4\in C_1.$
Then,
![]() $|\{v_3, v_4\}\cup C_2\cup B|=p+2.$
Since
$|\{v_3, v_4\}\cup C_2\cup B|=p+2.$
Since
![]() $\{v_3, v_4\}\cup C_2$
is an independent set and
$\{v_3, v_4\}\cup C_2$
is an independent set and
![]() $[C_2, B]=\emptyset ,$
we have
$[C_2, B]=\emptyset ,$
we have
![]() $|[\{v_3, v_4\}, B]|\ge p.$
However,
$|[\{v_3, v_4\}, B]|\ge p.$
However,
![]() $|B|=q.$
Hence,
$|B|=q.$
Hence,
![]() $N_B(v_j)=B$
for
$N_B(v_j)=B$
for
![]() $j=3,4.$
This shows that every vertex in
$j=3,4.$
This shows that every vertex in
![]() $C_1$
is adjacent to every vertex in
$C_1$
is adjacent to every vertex in
![]() $B.$
Consequently, every vertex in B has exactly q neighbours in
$B.$
Consequently, every vertex in B has exactly q neighbours in
![]() $D.$
$D.$
Choose any vertex
![]() $v_5\in B.$
Denote
$v_5\in B.$
Denote
![]() $M=N_D(v_5).$
We have
$M=N_D(v_5).$
We have
![]() $|M|=q.$
Since G is triangle-free and every vertex in B is adjacent to every vertex in
$|M|=q.$
Since G is triangle-free and every vertex in B is adjacent to every vertex in
![]() $C_1,$
the neighbourhood of any vertex in M is disjoint from
$C_1,$
the neighbourhood of any vertex in M is disjoint from
![]() $C_1.$
Thus, the q neighbours of any vertex of M in C are exactly the vertices of
$C_1.$
Thus, the q neighbours of any vertex of M in C are exactly the vertices of
![]() $C_2,$
implying that every vertex in M is adjacent to every vertex in
$C_2,$
implying that every vertex in M is adjacent to every vertex in
![]() $C_2.$
The neighbourhood of any vertex in
$C_2.$
The neighbourhood of any vertex in
![]() $C_2$
is
$C_2$
is
![]() $A\cup M.$
For the same reason, for any vertex
$A\cup M.$
For the same reason, for any vertex
![]() $v_6\in B$
with
$v_6\in B$
with
![]() $v_6\neq v_5,$
we must have
$v_6\neq v_5,$
we must have
![]() $N_D(v_6)=M.$
Hence, the neighbourhood of any vertex in M is
$N_D(v_6)=M.$
Hence, the neighbourhood of any vertex in M is
![]() $B\cup C_2.$
$B\cup C_2.$
We assert that
![]() $M=D.$
Otherwise, let
$M=D.$
Otherwise, let
![]() $v_7\in D\setminus M.$
Take a vertex
$v_7\in D\setminus M.$
Take a vertex
![]() $v_8\in C_1.$
Note that
$v_8\in C_1.$
Note that
![]() $B\cup C_2$
is an independent set of cardinality p and
$B\cup C_2$
is an independent set of cardinality p and
![]() $[v_7, B\cup C_2]=\emptyset .$
Denote
$[v_7, B\cup C_2]=\emptyset .$
Denote
![]() $R=\{v_7, v_8\}\cup B\cup C_2.$
Then,
$R=\{v_7, v_8\}\cup B\cup C_2.$
Then,
![]() $|R|=p+2$
and hence
$|R|=p+2$
and hence
![]() $G[R]$
has size at least
$G[R]$
has size at least
![]() $p.$
However, the size of
$p.$
However, the size of
![]() $G[R]$
is at most
$G[R]$
is at most
![]() $|[v_8, B]|+1=q+1<p,$
which is a contradiction. Finally, since G is p-regular, every vertex in A must be adjacent to every vertex in
$|[v_8, B]|+1=q+1<p,$
which is a contradiction. Finally, since G is p-regular, every vertex in A must be adjacent to every vertex in
![]() $C_1.$
Denote
$C_1.$
Denote
![]() $V_1=A, V_2=C_1, V_3=B, V_4=D, V_5=C_2$
and set
$V_1=A, V_2=C_1, V_3=B, V_4=D, V_5=C_2$
and set
![]() $V_6=V_1.$
Then, each
$V_6=V_1.$
Then, each
![]() $V_i$
is an independent set of cardinality
$V_i$
is an independent set of cardinality
![]() $q=p/2$
and every vertex in
$q=p/2$
and every vertex in
![]() $V_i$
is adjacent to every vertex in
$V_i$
is adjacent to every vertex in
![]() $V_{i+1}$
for
$V_{i+1}$
for
![]() $i=1,2,\ldots ,5.$
This proves that
$i=1,2,\ldots ,5.$
This proves that
![]() $G=C_5^{(q)}.$
Note that we have shown above that
$G=C_5^{(q)}.$
Note that we have shown above that
![]() $q=|D|\ge 3,$
implying that
$q=|D|\ge 3,$
implying that
![]() $p=2q\ge 6.$
$p=2q\ge 6.$
Conversely, let
![]() $H=C_5^{(q)}$
, where
$H=C_5^{(q)}$
, where
![]() $q=p/2$
and
$q=p/2$
and
![]() $p\ge 6$
is even. We will prove that H is a triangle-free
$p\ge 6$
is even. We will prove that H is a triangle-free
![]() $[p+2,p]$
-graph. Write
$[p+2,p]$
-graph. Write
![]() $H=H_1\vee H_2\vee H_3\vee H_4\vee H_5\vee H_1$
, where each
$H=H_1\vee H_2\vee H_3\vee H_4\vee H_5\vee H_1$
, where each
![]() $H_i=\overline {K_q}$
and
$H_i=\overline {K_q}$
and
![]() $\vee $
is the join operation on two vertex-disjoint graphs. If H contains a triangle, it must lie in
$\vee $
is the join operation on two vertex-disjoint graphs. If H contains a triangle, it must lie in
![]() $H[V(H_i)\cup V(H_{i+1})]$
for some i (
$H[V(H_i)\cup V(H_{i+1})]$
for some i (
![]() $H_6\triangleq H_1$
). However, this is a bipartite graph, containing no triangle.
$H_6\triangleq H_1$
). However, this is a bipartite graph, containing no triangle.
Let
![]() $U\subseteq V(H)$
with
$U\subseteq V(H)$
with
![]() $|U|=p+2.$
We need to show
$|U|=p+2.$
We need to show
![]() $e(H[U])\ge p.$
Denote
$e(H[U])\ge p.$
Denote
![]() $I=\{i \mid U\cap V(H_i)\neq \emptyset ,1\le i\le 5\}.$
Since
$I=\{i \mid U\cap V(H_i)\neq \emptyset ,1\le i\le 5\}.$
Since
![]() $|H_i|=q$
for
$|H_i|=q$
for
![]() $1\le i\le 5$
and
$1\le i\le 5$
and
![]() $|U|=p+2,$
we have
$|U|=p+2,$
we have
![]() $|I|\ge 3.$
Denote
$|I|\ge 3.$
Denote
![]() $x_i=|U\cap V(H_i)|$
for
$x_i=|U\cap V(H_i)|$
for
![]() $1\le i\le 5.$
Then,
$1\le i\le 5.$
Then,
![]() $0\le x_i\le q.$
We distinguish three cases.
$0\le x_i\le q.$
We distinguish three cases.
Case 1:
![]() $|I|=3.$
There are at least two consecutive integers in I (
$|I|=3.$
There are at least two consecutive integers in I (
![]() $1$
and
$1$
and
![]() $5$
are regarded as consecutive here). Without loss of generality, suppose
$5$
are regarded as consecutive here). Without loss of generality, suppose
![]() $1,2\in I.$
Then,
$1,2\in I.$
Then,
![]() $1\le x_1,\,x_2\le q$
and
$1\le x_1,\,x_2\le q$
and
![]() $x_1+x_2\ge p+2-q=q+2.$
Hence,
$x_1+x_2\ge p+2-q=q+2.$
Hence,
![]() $e(H[U])\ge x_1x_2\ge 2q=p.$
$e(H[U])\ge x_1x_2\ge 2q=p.$
Case 2:
![]() $|I|=4.$
Without loss of generality, suppose
$|I|=4.$
Without loss of generality, suppose
![]() $I=\{1,2,3,4\}.$
Then,
$I=\{1,2,3,4\}.$
Then,
![]() $e(H[U])=x_1x_2+x_2x_3+x_3x_4$
, where each
$e(H[U])=x_1x_2+x_2x_3+x_3x_4$
, where each
![]() $x_i$
is a positive integer and
$x_i$
is a positive integer and
![]() $x_1+x_2+x_3+x_4=p+2.$
Applying Lemma 2.1, we have
$x_1+x_2+x_3+x_4=p+2.$
Applying Lemma 2.1, we have
![]() $e(H[U])\ge (p+2)-1=p+1>p.$
$e(H[U])\ge (p+2)-1=p+1>p.$
Case 3:
![]() $|I|=5.$
Now,
$|I|=5.$
Now,
![]() $e(H[U])=x_1x_2+x_2x_3+x_3x_4+x_4x_5+x_5x_1$
, where each
$e(H[U])=x_1x_2+x_2x_3+x_3x_4+x_4x_5+x_5x_1$
, where each
![]() $x_i$
is a positive integer and
$x_i$
is a positive integer and
![]() $x_1+x_2+x_3+x_4+x_5=p+2.$
Applying Lemma 2.2, we have
$x_1+x_2+x_3+x_4+x_5=p+2.$
Applying Lemma 2.2, we have
![]() $e(H[U])\ge 2(p+2)-5=2p-1>p.$
$e(H[U])\ge 2(p+2)-5=2p-1>p.$
In every case, H is a
![]() $[p+2,p]$
-graph. This completes the proof.
$[p+2,p]$
-graph. This completes the proof.
Theorem 2.5. Every
![]() $2$
-connected
$2$
-connected
![]() $[4,2]$
-graph of order at least
$[4,2]$
-graph of order at least
![]() $7$
is pancyclic.
$7$
is pancyclic.
Proof. Let G be a
![]() $2$
-connected
$2$
-connected
![]() $[4,2]$
-graph of order at least
$[4,2]$
-graph of order at least
![]() $7.$
Since G is
$7.$
Since G is
![]() $2$
-connected,
$2$
-connected,
![]() $\delta (G)\ge 2.$
By the case
$\delta (G)\ge 2.$
By the case
![]() $p=2$
of Lemma 2.4, G contains a triangle
$p=2$
of Lemma 2.4, G contains a triangle
![]() $C_3.$
Then, successively applying Theorem 1.3, we deduce that G is pancyclic.
$C_3.$
Then, successively applying Theorem 1.3, we deduce that G is pancyclic.
Remark 2.6. The Chvátal–Erdős theorem on Hamiltonian graphs [Reference Bondy1, Reference Chvátal and Erdős4, Reference West8] states that for a graph
![]() $G,$
if
$G,$
if
![]() $\kappa (G)\ge \alpha (G)$
, then G is Hamiltonian, where
$\kappa (G)\ge \alpha (G)$
, then G is Hamiltonian, where
![]() $\kappa $
and
$\kappa $
and
![]() $\alpha $
denote the connectivity and independence number, respectively. Bondy [Reference Bondy2] proved that if a graph satisfies Ore’s condition, then it satisfies the Chvátal–Erdős condition. A computer search for graphs of lower orders shows that there are many graphs which satisfy the condition in Theorem 2.5, but do not satisfy the Chvátal–Erdős condition. There are exactly
$\alpha $
denote the connectivity and independence number, respectively. Bondy [Reference Bondy2] proved that if a graph satisfies Ore’s condition, then it satisfies the Chvátal–Erdős condition. A computer search for graphs of lower orders shows that there are many graphs which satisfy the condition in Theorem 2.5, but do not satisfy the Chvátal–Erdős condition. There are exactly
![]() $398$
such graphs of order
$398$
such graphs of order
![]() $9.$
For every integer
$9.$
For every integer
![]() $n\ge 7$
, we give an example. Let
$n\ge 7$
, we give an example. Let
![]() $G_1=K_{n-3}^{-}$
be the graph obtained from
$G_1=K_{n-3}^{-}$
be the graph obtained from
![]() $K_{n-3}$
by deleting one edge
$K_{n-3}$
by deleting one edge
![]() $xy$
and let
$xy$
and let
![]() $G_2=uvw$
be a triangle that is vertex-disjoint from
$G_2=uvw$
be a triangle that is vertex-disjoint from
![]() $G_1.$
Construct a graph
$G_1.$
Construct a graph
![]() $Z_n$
from
$Z_n$
from
![]() $G_1$
and
$G_1$
and
![]() $G_2$
by adding two edges
$G_2$
by adding two edges
![]() $xu$
and
$xu$
and
![]() $yv.$
The graph
$yv.$
The graph
![]() $Z_9$
is depicted in Figure 3.
$Z_9$
is depicted in Figure 3.

Figure 3 The graph
![]() $Z_9$
.
$Z_9$
.
Clearly,
![]() $Z_n$
is a
$Z_n$
is a
![]() $2$
-connected
$2$
-connected
![]() $[4,2]$
-graph of order
$[4,2]$
-graph of order
![]() $n,$
but
$n,$
but
![]() $2=\kappa (Z_n)<\alpha (Z_n)=3.$
$2=\kappa (Z_n)<\alpha (Z_n)=3.$