Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T16:20:12.291Z Has data issue: false hasContentIssue false
  • English
  • Français

SUCCESSIVE RADII OF FAMILIES OF CONVEX BODIES

Part of: General convexity

Published online by Cambridge University Press:  15 December 2014

BERNARDO GONZÁLEZ ,
MARÍA A. HERNÁNDEZ CIFRE  and
AICKE HINRICHS
BERNARDO GONZÁLEZ
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, 30100-Murcia, Spain email [email protected]
MARÍA A. HERNÁNDEZ CIFRE*
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, 30100 Murcia, Spain email [email protected]
AICKE HINRICHS
Affiliation:
Institut für Analysis, Johannes Kepler Universität Linz, Altenberger Str. 69, 4040 Linz, Austria email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study properties of the so-called inner and outer successive radii of special families of convex bodies. First we consider the balls of the 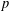$p$-norms, for which we show that the precise value of the outer (inner) radii when 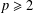$p\geq 2$ (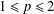$1\leq p\leq 2$), as well as bounds in the contrary case 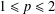$1\leq p\leq 2$ (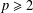$p\geq 2$), can be obtained as consequences of known results on Gelfand and Kolmogorov numbers of identity operators between finite-dimensional normed spaces. We also prove properties that successive radii satisfy when we restrict to the families of the constant width sets and the 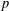$p$-tangential bodies.

Keywords

successive inner and outer radiiGelfand and Kolmogorov numbersp-ballsconstant width setstangential bodies

MSC classification

Primary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Secondary: 52A40: Inequalities and extremum problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 331 - 344
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Ball, K., ‘Ellipsoids of maximal volume in convex bodies’, Geom. Dedicata 41 (1992), 241–250.CrossRefGoogle Scholar
Betke, U. and Henk, M., ‘Estimating sizes of a convex body by successive diameters and widths’, Mathematika 39(2) (1992), 247–257.Google Scholar
Betke, U. and Henk, M., ‘A generalization of Steinhagen’s theorem’, Abh. Math. Semin. Univ. Hambg. 63 (1993), 165–176.CrossRefGoogle Scholar
Betke, U., Henk, M. and Tsintsifa, L., ‘Inradii of simplices’, Discrete Comput. Geom. 17(4) (1997), 365–375.Google Scholar
Bonnesen, T. and Fenchel, W., Theory of Convex Bodies (eds. Boron, L., Christenson, C. and Smith, B.) (BCS Associates, Moscow, ID, 1987).Google Scholar
Brandenberg, R., ‘Radii of convex bodies’, PhD Thesis, Technische Universität München, 2002.Google Scholar
Brandenberg, R., ‘Radii of regular polytopes’, Discrete Comput. Geom. 33(1) (2005), 43–55.CrossRefGoogle Scholar
Brandenberg, R., Dattasharma, A., Gritzmann, P. and Larman, D., ‘Isoradial bodies’, Discrete Comput. Geom. 32(4) (2004), 447–457.CrossRefGoogle Scholar
Brandenberg, R. and Theobald, T., ‘Radii of simplices and some applications to geometric inequalities’, Beitr. Algebra Geom. 45(2) (2004), 581–594.Google Scholar
Carl, B. and Stephani, I., Entropy, Compactness and Approximation of Operators (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Chakerian, G. D. and Groemer, H., ‘Convex bodies of constant width’, in: Convexity and Its Applications (eds. Gruber, P. M. and Wills, J. M.) (Birkhäuser, Basel, 1983), 49–96.Google Scholar
Eggleston, H. G., Convexity, Cambridge Tracts in Mathematics and Mathematical Physics, 47 (Cambridge University Press, New York, 1958).CrossRefGoogle Scholar
Everett, H., Stojmenovic, I., Valtr, P. and Whitesides, S., ‘The largest k-ball in a d-dimensional box’, Comput. Geom. 11(2) (1998), 59–67.CrossRefGoogle Scholar
Favard, J., ‘Sur les corps convexes’, J. Math. Pures Appl. 12(9) (1933), 219–282.Google Scholar
Gluskin, E. D., ‘Norms of random matrices and diameters of finite-dimensional sets’, Mat. Sb. (N.S.) 120(162) (1983), 180–189 (in Russian).Google Scholar
Gritzmann, P. and Klee, V., ‘Inner and outer j-radii of convex bodies in finite-dimensional normed spaces’, Discrete Comput. Geom. 7 (1992), 255–280.Google Scholar
Henk, M., ‘Ungleichungen für sukzessive Minima und verallgemeinerte In- und Umkugelradien’, PhD Thesis, University of Siegen, 1991.Google Scholar
Henk, M., ‘A generalization of Jung’s theorem’, Geom. Dedicata 42 (1992), 235–240.CrossRefGoogle Scholar
Henk, M. and Hernández Cifre, M. A., ‘Intrinsic volumes and successive radii’, J. Math. Anal. Appl. 343(2) (2008), 733–742.Google Scholar
Hinrichs, A., ‘Approximation numbers of identity operators between symmetric Banach sequence spaces’, J. Approx. Theory 118 (2002), 305–315.Google Scholar
Hinrichs, A. and Michels, C., ‘Gelfand numbers of identity operators between symmetric sequence spaces’, Positivity 10 (2006), 111–133.Google Scholar
König, H., Eigenvalue Distributions of Compact Operators (Birkhäuser, Basel, 1986).Google Scholar
Pietsch, A., ‘s-numbers of operators in Banach spaces’, Studia Math. 51 (1974), 201–223.CrossRefGoogle Scholar
Pietsch, A., Operator Ideals (VEB Deutscher Verlag der Wissenschaften, Berlin, 1978).Google Scholar
Pietsch, A., Eigenvalues and s-Numbers (Cambridge University Press, Cambridge, 1987).Google Scholar
Pinkus, A., N-Widths in Approximation Theory (Springer, Berlin, 1985).CrossRefGoogle Scholar
Puhov, S. V., ‘Inequalities for the Kolmogorov and Bernšteĭn widths in Hilbert space’, Mat. Zametki 25(4) (1979), 619–628; 637 (in Russian); translation Math. Notes 25 (4 (1979), 320–326.Google Scholar
Sangwine-Yager, J. R., ‘Inner parallel bodies and geometric inequalities’, PhD Thesis, University of California Davis, 1978.Google Scholar
Schneider, R., Convex Bodies: The Brunn-Minkowski Theory, 2nd expanded edn (Cambridge University Press, Cambridge, 2014).Google Scholar
Steckin, S. B., ‘On the best approximation of given classes of functions by arbitrary polynomials’, Uspekhi Mat. Nauk 9 (1954), 133–134 (in Russian).Google Scholar