Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T02:26:07.328Z Has data issue: false hasContentIssue false
  • English
  • Français

A STRUCTURED INVERSE SPECTRUM PROBLEM FOR INFINITE GRAPHS AND UNBOUNDED OPERATORS

Part of: General theory of linear operators Graph theory Basic linear algebra

Published online by Cambridge University Press:  15 August 2018

EHSSAN KHANMOHAMMADI Open the ORCID record for EHSSAN KHANMOHAMMADI [Opens in a new window]
EHSSAN KHANMOHAMMADI*
Affiliation:
Lancaster, PA 17603, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 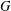$G$ be an infinite graph on countably many vertices and let 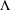$\unicode[STIX]{x1D6EC}$ be a closed, infinite set of real numbers. We establish the existence of an unbounded self-adjoint operator whose graph is 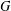$G$ and whose spectrum is 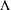$\unicode[STIX]{x1D6EC}$.

Keywords

inverse spectrum probleminfinite graphisospectralunbounded operator

MSC classification

Primary: 05C63: Infinite graphs
Secondary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.) 15A29: Inverse problems 47A10: Spectrum, resolvent
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 3 , December 2018 , pp. 363 - 371
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Hall, B. C., Quantum Theory for Mathematicians, Graduate Texts in Mathematics, 267 (Springer, New York, 2013).Google Scholar
Hassani Monfared, K. and Khanmohammadi, E., ‘A structured inverse spectrum problem for infinite graphs’, Linear Algebra Appl. 539 (2018), 28–43.Google Scholar
Kato, T., Perturbation Theory for Linear Operators (Springer, New York, 1995).Google Scholar
Mohar, B., ‘The spectrum of an infinite graph’, Linear Algebra Appl. 48 (1982), 245–256.Google Scholar
Schmüdgen, K., Unbounded Self-adjoint Operators on Hilbert Space, Graduate Texts in Mathematics, 265 (Springer, Dordrecht, 2012).Google Scholar