Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-25T19:27:42.536Z Has data issue: false hasContentIssue false
  • English
  • Français

THE STRONG DUAL OF MEASURE ALGEBRAS WITH CERTAIN LOCALLY CONVEX TOPOLOGIES

Part of: Topological algebras, normed rings and algebras, Banach algebras Abstract harmonic analysis Topological linear spaces and related structures

Published online by Cambridge University Press:  08 April 2013

HOSSEIN JAVANSHIRI  and
RASOUL NASR-ISFAHANI
HOSSEIN JAVANSHIRI
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran email [email protected]
RASOUL NASR-ISFAHANI*
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran email [email protected] School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box: 19395-5746, Tehran, Iran
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a locally compact group 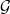$ \mathcal{G} $, we introduce and study a class of locally convex topologies $\tau $ on the measure algebra 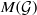$M( \mathcal{G} )$ of 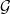$ \mathcal{G} $. In particular, we show that the strong dual of 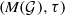$(M( \mathcal{G} ), \tau )$ can be identified with a closed subspace of the Banach space 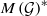$M\mathop{( \mathcal{G} )}\nolimits ^{\ast } $; we also investigate some properties of the locally convex space 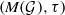$(M( \mathcal{G} ), \tau )$.

Keywords

measure algebrastrict topologylocally compact grouplocally convex space

MSC classification

Secondary: 43A10: Measure algebras on groups, semigroups, etc. 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc. 46A03: General theory of locally convex spaces 46H05: General theory of topological algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 3 , June 2013 , pp. 353 - 365
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Buck, R. C., ‘Bounded continuous functions on a locally compact space’, Michigan Math. J. 5 (1958), 95–104.CrossRefGoogle Scholar
Busby, R. C., ‘Double centralizers and extension of C∗-algebras’, Trans. Amer. Math. Soc. 132 (1968), 79–99.Google Scholar
Davenport, J. W., ‘The strict dual of B∗-algebras’, Proc. Amer. Math. Soc. 65 (1977), 309–312.Google Scholar
Ferrera, J. and Prieto, A., ‘The strict topology on spaces of bounded holomorphic functions’, Bull. Aust. Math. Soc. 49 (1994), 249–256.CrossRefGoogle Scholar
Grosser, M. and Losert, V., ‘The norm-strict bidual of a Banach algebra and the dual of ${C}_{u} ( \mathcal{G} )$’, Manuscripta Math. 45 (1984), 127–146.CrossRefGoogle Scholar
Gulick, D., ‘Duality theory for the strict topology’, Studia Math. 49 (1974), 195–208.CrossRefGoogle Scholar
Hewitt, E. and Ross, K., Abstract Harmonic Analysis I (Springer, Berlin, 1970).Google Scholar
Isik, N., Pym, J. and Ülger, A., ‘The second dual of the group algebra of a compact group’, J. Lond. Math. Soc. 35 (1987), 135–148.CrossRefGoogle Scholar
Lau, A. T. and Pym, J., ‘Concerning the second dual of the group algebra of a locally compact group’, J. Lond. Math. Soc. 41 (1990), 445–460.CrossRefGoogle Scholar
Laursen, K. B. and Neumann, M., An Introduction to Local Spectral Theory (Clarendon Press, Oxford, 2000).CrossRefGoogle Scholar
Mehdipour, M. J. and Nasr-Isfahani, R., ‘Compact left multipliers on Banach algebras related to locally compact groups’, Bull. Aust. Math. Soc. 79 (2009), 227–238.CrossRefGoogle Scholar
Robertson, J. M. and Wiser, H. C., ‘A note on polar topologies’, Canad. Math. Bull. 11 (1968), 607–609.CrossRefGoogle Scholar
Sentilles, F. and Taylor, D., ‘Factorization in Banach algebras and the general strict topology’, Trans. Amer. Math. Soc. 142 (1969), 141–152.CrossRefGoogle Scholar
Shapiro, J. H., ‘The bounded weak star topology and the general strict topology’, J. Funct. Anal. 8 (1971), 275–286.CrossRefGoogle Scholar
Singh, A. I., ‘${ L}_{0}^{\infty } \mathop{( \mathcal{G} )}\nolimits ^{\ast } $ as the second dual of the group algebra ${L}^{1} ( \mathcal{G} )$ with a locally convex topology’, Michigan Math. J. 46 (1999), 143–150.CrossRefGoogle Scholar
Sreider, Yu. A., ‘The structure of maximal ideals in rings of measures with convolution’, Math. Sbornik 27 (1950), 297–318.Google Scholar
Swartz, C., An Introduction to Functional Analysis, Pure and Applied Mathematics, 157 (Marcel Dekker, New York, 1992).Google Scholar
Taylor, D. C., ‘The strict topology for double centralizer algebras’, Trans. Amer. Math. Soc. 150 (1970), 633–643.CrossRefGoogle Scholar
Wendel, J. G., ‘Left centralizers and isomorphisms of group algebras’, Pacific J. Math. 2 (1952), 251–261.CrossRefGoogle Scholar
Wheeler, R. F., ‘A survey of Baire measures and strict topologies’, Expo. Math. 1 (1983), 97–190.Google Scholar
Wong, J. C., ‘Abstract harmonic analysis of generalized functions on locally compact semigroups with applications to invariant means’, J. Aust. Math. Soc. 23 (1977), 84–94.CrossRefGoogle Scholar
Wong, J. C., ‘Convolution and separate continuity’, Pacific J. Math 75 (1978), 601–611.CrossRefGoogle Scholar