Hostname: page-component-6bf8c574d5-r8w4l Total loading time: 0 Render date: 2025-03-09T14:51:58.456Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong convergence of selections implied by weak

Published online by Cambridge University Press:  17 April 2009

Tadeusz Rzezuchowski
Tadeusz Rzezuchowski
Affiliation:
Institute of Mathematics, Warsaw Technical University, Pl.J.Robotniczej, 100-661 Warsaw, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

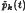In some situations weak convergence in L1, implies strong convergence. Let P, L: T → C∘(ℝd) be measurable multifunctions (C∘(ℝd) being the set of closed, convex subsets of ℝd) the values L(t) affine sets and W(t) = P(t) ∩ L(t) extremal faces of P(t). Let pk be integrable selections of P, the projection of pk,(t) on L(t) and pk(t) on W(t). We prove that if 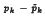converges weakly to zero then pk − 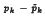k converges to zero in measure. We give also some extensions of this theorem. As applications to differential inclusions we investigate convergence of derivatives of convergent sequences of solutions and we describe solutions which are in some sense isolated. Finally we discuss what can be said about control functions u when the corresponding trajectories of ẋ = f(t, x, u) are convergent to some trajectory.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 39 , Issue 2 , April 1989 , pp. 201 - 214
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Aubin, J.P. and Cellina, A., Differential inclusions (Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1984).CrossRefGoogle Scholar
[2]Balder, E.J., ‘On weak convergence implying strong convergence in L 1-spaces’, Bull. Austral. Math. Soc. 33 (1986), 363–368.CrossRefGoogle Scholar
[3]Castaing, C. and Valadier, M., Convex analysis and measurable multifunctions (Springer-Verlag, Berlin, Heidelberg, New York, 1977).CrossRefGoogle Scholar
[4]Floret, K., Weakly compact sets (Springer-Verlag, Berlin, Heidelberg, New York, 1988).Google Scholar
[5]Jarnik, J. and Kurzweil, J., ‘On conditions on right hand sides of differential relations’, Casopis Pest. Mat. 102 (1977), 334–349.CrossRefGoogle Scholar
[6]Olech, C., ‘Extremal solutions of a control system’, J. Differential Equations 2 (1966), 74–101.CrossRefGoogle Scholar
[7]Olech, C., ‘Existence theory in optimal control’, in Control theory and topics in functional analysis, I (Vienna, 1976). pp. 291–328.Google Scholar
[8]Rockafellar, R.T., Convex analysis (Princeton University Press, 1970).CrossRefGoogle Scholar
[9]Rzezuchowski, T., ‘Scorza-Dragoni type theorem for upper semicontinuous multivalued functions’, Bull. Acad. Polon. Sci. Sér. Sci. Math. 28 (1980), 61–66.Google Scholar
[10]Scorza-Dragoni, G., ‘Un teorema sulle funzioni continue rispetto ad una e misurabili respetto ad un'altra variabile’, Rend. Sem. Mat. Univ. Padova 17 (1948), 102–108.Google Scholar
[11]Visintin, A., ‘Strong convergence results related to strict convexity’, Comm. Partial Differential Equations 9 (1984), 439–466.CrossRefGoogle Scholar