Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-04T23:57:45.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Spaces with homogeneous norms

Published online by Cambridge University Press:  17 April 2009

A.J. Pryde
A.J. Pryde
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Canada M5S IA1.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Spaces with homogeneous norms are closely related to the Beppo Levi spaces of Deny and Lions, to spaces of Riesz potentials, and to Sobolev spaces. In this paper we survey the literature on them, give a broad extension of their definition, and present their basic theory. Many of the properties of Sobolev spaces have their analogues. In fact, the two families are locally equivalent. Spaces with homogeneous norms are especially suited to the study of boundary value problems on 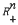for homogeneous elliptic operators with constant coefficients. We will use them extensively in a forthcoming paper to study elliptic partial differential equations with mixed boundary conditions on a smoothly bounded domain.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 21 , Issue 2 , May 1980 , pp. 189 - 205
Copyright
Copyright © Australian Mathematical Society 1980

References

[1]Agranovich, M.S., “Elliptic singular integro-differential operators”, Russian Math. Surveys 20 (1965), no. 5, 1–121.CrossRefGoogle Scholar
[2]Aronszajn, N. and Smith, K.T., “Functional spaces and functional completion”, Ann. Inst. Fourier (Grenoble) 6 (1955 et 1956), 125–185.CrossRefGoogle Scholar
[3]Aronszajn, N. and Smith, K.T., “Theory of Bessel potentials. Part I”, Ann. Inst. Fourier (Grenoble) 11 (1961), 385–475.CrossRefGoogle Scholar
[4]Deny, J. et Lions, J.L., “Les espaces du type de Beppo Levi”, Ann. Inst. Fourier (Grenoble) 5 (1953 et 1954), 305–370.CrossRefGoogle Scholar
[5]Gunning, Robert C., Rossi, Hugo, Analytic functions of several complex variables (Prentice-Hall, Englewood Cliffs, New Jersey, 1965).Google Scholar
[6]Hörmander, L. et Lions, J.L., “Sur le complétion par rapport à une intégrale de Dirichlet”, Math. Scand. 4 (1956), 259–270.CrossRefGoogle Scholar
[7]Lions, J.L., Magenes, E., Problèmes aux limites non homogèes et applications, Tome I (Dunod, Paris, 1968). English translation: Non-homogeneous boundary value problems and applications, Volume I (translated by P. Kenneth. Die Grundlehren der mathematischen Wissenschaften, 181. Springer-Verlag, Berlin, Heidelberg, New York, 1972).Google Scholar
[8]Malgrange, B., “Sur l'intégrale de Dirichlet”, Math. Scand. 4 (1956), 271–275.CrossRefGoogle Scholar
[9]Nečas, Jindřich, Les méthodes directes en théorie des équations elliptiques (Masson, Paris; Academia, Prague, 1967).Google Scholar
[10]Peetre, Jaak, “Another approach to elliptic boundary problems”, Comm. Pure Appl. Math. 14 (1961), 711–731.CrossRefGoogle Scholar
[11]Peetre, Jaak, “Mixed problems for higher order elliptic equations in two variables, I”, Ann. Scuola Norm. Sup. Pisa (3) 15 (1961), 337–353.Google Scholar
[12]Peetre, Jaak, “Mixed problems for higher order elliptic equations in two variables, II”, Ann. Scuola Norm. Sup. Pisa (3) 17 (1963), 1–12.Google Scholar
[13]van der Poorten, A.J., “Some determinants that should be better known”, J. Austral. Math. Soc. Ser. A 21 (1976), 278–288.CrossRefGoogle Scholar
[14]Pryde, A.J., “Elliptic partial differential equations with mixed boundary conditions” (PhD thesis, Macquarie University, New South Wales, 1976). See also: Abstract, Bull. Austral. Math. Soc. 15 (1976), 475–476.CrossRefGoogle Scholar
[15]Pryde, A.J., “Second order elliptic equations with mixed boundary conditions”, Bull. Amer. Math. Soc. 83 (1977), 391–393.CrossRefGoogle Scholar
[16]Pryde, A.J., “The five lemma for Banach spaces”, Proc. Amer. Math. Soc. 65 (1977), 37–43.CrossRefGoogle Scholar
[17]Shamir, E., “Mixed boundary value problems for elliptic equations in the plane. The Lp theory”, Ann. Scuola Norm. Sup. Pisa (3) 17 (1963), 117–139.Google Scholar
[18]Shamir, Eliahu, “Reduced Hilbert transforms and singular integral equations”, J. Analyse Math. 12 (1964), 277–305.CrossRefGoogle Scholar
[19]Shamir, Eliahu, “Elliptic systems of singular integral operators. I. The half-space case”, Trans. Amer. Math. Soc 127 (1967), 107–124.CrossRefGoogle Scholar
[20]Stein, Elias M., Singular integrals and differentiability properties of functions (Princeton Mathematical Series, 30. Princeton University Press, Princeton, New Jersey, 1970).Google Scholar
[21]Vishik, M.I. and Eskin, G.I., “Equations in convolutions in a bounded region”, Russian Math. Surveys 20 (1965), no. 3, 85–151.CrossRefGoogle Scholar
[22]Vishik, M.I. and Eskin, G.I., “Elliptic equations in convolution in a bounded domain and their applications”, Russian Math. Surveys 22 (1967), no. 1, 13–75.CrossRefGoogle Scholar