Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T15:38:44.461Z Has data issue: false hasContentIssue false
  • English
  • Français

SPACELIKE CAPILLARY SURFACES IN THE LORENTZ–MINKOWSKI SPACE

Part of: Classical differential geometry

Published online by Cambridge University Press:  09 August 2011

JUNCHEOL PYO  and
KEOMKYO SEO
JUNCHEOL PYO
Affiliation:
Department of Mathematics, Pusan National University, Busan 609-735, Korea (email: [email protected])
KEOMKYO SEO*
Affiliation:
Department of Mathematics, Sookmyung Women’s University, Hyochangwongil 52, Yongsan-ku, Seoul 140-742, Korea (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a compact spacelike constant mean curvature surface with nonempty boundary in the three-dimensional Lorentz–Minkowski space, we introduce a rotation index of the lines of curvature at the boundary umbilical point, which was developed by Choe [‘Sufficient conditions for constant mean curvature surfaces to be round’, Math. Ann.323(1) (2002), 143–156]. Using the concept of the rotation index at the interior and boundary umbilical points and applying the Poincaré–Hopf index formula, we prove that a compact immersed spacelike disk type capillary surface with less than four vertices in a domain of 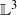bounded by (spacelike or timelike) totally umbilical surfaces is part of a (spacelike) plane or a hyperbolic plane. Moreover, we prove that the only immersed spacelike disk type capillary surface inside a de Sitter surface in 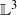is part of (spacelike) plane or a hyperbolic plane.

Keywords

capillary surfacesspacelike surfacesconstant mean curvature

MSC classification

Secondary: 53A10: Minimal surfaces, surfaces with prescribed mean curvature
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 84 , Issue 3 , December 2011 , pp. 362 - 371
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

Footnotes

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2010-0022951 and 2010-0004246).

References

[1]Alías, L., López, R. and Palmer, B., ‘Stable constant mean curvature surfaces with circular boundary’, Proc. Amer. Math. Soc. 127(4) (1999), 1195–1200.CrossRefGoogle Scholar
[2]Alías, L., López, R. and Pastor, J., ‘Compact spacelike surfaces with constant mean curvature in the Lorentz–Minkowski 3-space’, Tohoku Math. J. 50 (1998), 491–501.CrossRefGoogle Scholar
[3]Alías, L. and Pastor, J., ‘Constant mean curvature spacelike hypersurfaces with spherical boundary in the Lorentz–Minkowski space’, J. Geom. Phys. 28(1–2) (1998), 85–93.CrossRefGoogle Scholar
[4]Alías, L. and Pastor, J., ‘Spacelike surfaces of constant mean curvature with free boundary in the Minkowski space’, Classical Quantum Gravity 16 (1999), 1323–1331.CrossRefGoogle Scholar
[5]Choe, J., ‘Sufficient conditions for constant mean curvature surfaces to be round’, Math. Ann. 323(1) (2002), 143–156.CrossRefGoogle Scholar
[6]Choquet-Bruhat, Y. and York, J., The Cauchy Problem. General Relativity and Gravitation, Vol. 1 (Plenum, New York, 1980), pp. 99–172.Google Scholar
[7]Earp, R., Brito, F., Meeks, W. and Rosenberg, H., ‘Structure theorems for constant mean curvature surfaces bounded by a planar curve’, Indiana Univ. Math. J. 40(1) (1991), 333–343.CrossRefGoogle Scholar
[8]Finn, R., Equilibrium Capillary Surfaces, Grundlehren der Mathematischen Wissenschaften, 284 (Springer, New York, 1986).CrossRefGoogle Scholar
[9]Hopf, H., Differential Geometry in the Large, Lecture Notes in Mathematics, 1000 (Springer, Berlin, 1989).CrossRefGoogle Scholar
[10]Kobayashi, O., ‘Maximal surfaces in the 3-dimensional Minkowski space L 3’, Tokyo J. Math. 6(2) (1983), 297–309.CrossRefGoogle Scholar
[11]Koiso, M., ‘Symmetry of hypersurfaces of constant mean curvature with symmetric boundary’, Math. Z. 191(4) (1986), 567–574.CrossRefGoogle Scholar
[12]López, F., López, R. and Souam, R., ‘Maximal surfaces of Riemann type in Lorentz–Minkowski space ’, Michigan Math. J. 47(3) (2000), 469–497.CrossRefGoogle Scholar
[13]López, R. and Montiel, S., ‘Constant mean curvature discs with bounded area’, Proc. Amer. Math. Soc. 123(5) (1995), 1555–1558.CrossRefGoogle Scholar
[14]López, R. and Montiel, S., ‘Constant mean curvature surfaces with planar boundary’, Duke Math. J. 85(3) (1996), 583–604.CrossRefGoogle Scholar
[15]Marsden, J. and Tipler, F., ‘Maximal hypersurfaces and foliations of constant mean curvature in general relativity’, Phys. Rep. 66(3) (1980), 109–139.CrossRefGoogle Scholar
[16]Nitsche, J., ‘Stationary partitioning of convex bodies’, Arch. Ration. Mech. Anal. 89(1) (1985), 1–19.CrossRefGoogle Scholar
[17]O’Neill, B., Semi-Riemannian Geometry with Application to Relativity, Pure and Applied Mathematics, 130 (Academic Press, New York, 1983).Google Scholar
[18]Ratcliffe, J., Foundations of Hyperbolic Manifolds, 2nd edn, Graduate Texts in Mathematics, 149 (Springer, New York, 2006).Google Scholar
[19]Ros, A. and Rosenberg, H., ‘Constant mean curvature surfaces in a half-space of R 3 with boundary in the boundary of the half-space’, J. Differential Geom. 44(4) (1996), 807–817.CrossRefGoogle Scholar
[20]Ros, A. and Souam, R., ‘On stability of capillary surfaces in a ball’, Pacific J. Math. 178(2) (1997), 345–361.CrossRefGoogle Scholar
[21]Spivak, M., A Comprehensive Introduction to Differential Geometry, Vol. III (Publish or Perish, Berkeley, CA, 1979).Google Scholar