Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Jianlin
2006.
Two-Weight Norm Inequality for Imaginary Powers of a Laplace Operator.
Journal of Systems Science and Complexity,
Vol. 19,
Issue. 3,
p.
403.
Wang, Hua
2015.
The Boundedness of Some Integral Operators on Weighted Hardy Spaces Associated with Schrödinger Operators.
Journal of Function Spaces,
Vol. 2015,
Issue. ,
p.
1.
GUNAWAN, HENDRA
HAKIM, DENNY IVANAL
NAKAI, EIICHI
and
SAWANO, YOSHIHIRO
2018.
THE HARDY AND HEISENBERG INEQUALITIES IN MORREY SPACES.
Bulletin of the Australian Mathematical Society,
Vol. 97,
Issue. 3,
p.
480.


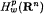 to weighted Lebesgue spaces
to weighted Lebesgue spaces 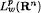 where 0 <
where 0 < 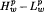 estimates for these operators when 0 <
estimates for these operators when 0 < 