Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Donepudi, Ravi
Li, Junxian
and
Zaharescu, Alexandru
2017.
Exact evaluation of second moments associated with some families of curves over a finite field.
Finite Fields and Their Applications,
Vol. 48,
Issue. ,
p.
331.


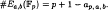
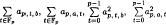 and
and 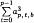 for primes
for primes