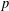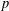Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abdollahi, Alireza
Guedri, Maria
and
Guerboussa, Yassine
2017.
Non-triviality of Tate cohomology for certain classes of finitep-groups.
Communications in Algebra,
Vol. 45,
Issue. 12,
p.
5188.
Ruscitti, Marco
Legarreta, Leire
and
Yadav, Manoj K.
2017.
Non-inner automorphisms of order p in finite p-groups of coclass 3.
Monatshefte für Mathematik,
Vol. 183,
Issue. 4,
p.
679.
Garg, Rohit
and
Singh, Mandeep
2021.
Finite p-groups with non-cyclic center have a non-inner automorphism of order p.
Archiv der Mathematik,
Vol. 117,
Issue. 2,
p.
129.
Zhang, Qinhai
2022.
Some unsolvable conjectures in finite p-groups.
Frontiers of Mathematics in China,
Vol. 17,
Issue. 1,
p.
1.