Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T04:38:23.785Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME OBSERVATIONS AND SPECULATIONS ON PARTITIONS INTO d-TH POWERS

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  28 January 2021

MACIEJ ULAS Open the ORCID record for MACIEJ ULAS [Opens in a new window]
MACIEJ ULAS*
Affiliation:
Institute of Mathematics, Faculty of Mathematics and Computer Science, Jagiellonian University, Łojasiewicza 6, 30 – 348Kraków, Poland
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this article is to provoke discussion concerning arithmetic properties of the function 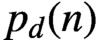$p_{d}(n)$ counting partitions of a positive integer n into dth powers, where 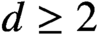$d\geq 2$ . Apart from results concerning the asymptotic behaviour of 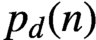$p_{d}(n)$ , little is known. In the first part of the paper, we prove certain congruences involving functions counting various types of partitions into dth powers. The second part of the paper is experimental and contains questions and conjectures concerning the arithmetic behaviour of the sequence 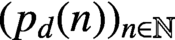$(p_{d}(n))_{n\in \mathbb {N}}$ , based on computations of 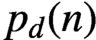$p_{d}(n)$ for 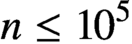$n\leq 10^5$ for 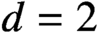$d=2$ and 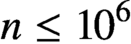$n\leq 10^{6}$ for 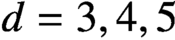$d=3, 4, 5$ .

Keywords

identitiesnumerical computationspartitions into powers

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 406 - 414
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Australian Mathematical Publishing Association Inc. 2021.

Footnotes

The research of the author is supported by the grant of the National Science Centre (NCN), Poland, No. UMO-2019/34/E/ST1/00094.

References

Andrews, G. E., The Theory of Partitions (Cambridge University Press, Cambridge, 1998).Google Scholar
Andrews, G. E., ‘Partitions: at the interface of $q$ -series and modular forms’, Ramanujan J. 7 (2003), 385–400.10.1023/A:1026224002193CrossRefGoogle Scholar
Ciolan, A., ‘Asymptotics and inequalities for partitions into squares’, Int. J. Number Theory 16(1) (2020), 121–143.CrossRefGoogle Scholar
DeSalvo, S. and Pak, I., ‘Log-concavity of the partition function’, Ramanujan J. 38 (2015), 61–73.CrossRefGoogle Scholar
Gafni, A., ‘Power partitions’, J. Number Theory 163 (2016), 19–42.10.1016/j.jnt.2015.11.004CrossRefGoogle Scholar
Hardy, G. H. and Ramanujan, S., ‘Asymptotic formulae in combinatory analysis’, Proc. Lond. Math. Soc. 2 (1918), 75–115.10.1112/plms/s2-17.1.75CrossRefGoogle Scholar
Hou, Q.-H. and Zhang, Z.-R., ‘ $r$ -log-concavity of partition functions’, Ramanujan J. 48 (2019), 117–129.10.1007/s11139-017-9975-5CrossRefGoogle Scholar
Tenenbaum, G., Wu, J. and Li, Y.-L., ‘Power partitions and saddle-point method’, J. Number Theory 204 (2019), 435–445.CrossRefGoogle Scholar
Vaughan, R. C., ‘Squares: additive questions and partitions’, Int. J. Number Theory 11(5) (2015), 1–43.10.1142/S1793042115400096CrossRefGoogle Scholar
Wright, E. M., ‘Asymptotic partition formulae. III. Partitions into $k$ -th powers’, Acta Math. 63(1) (1934), 143–191.CrossRefGoogle Scholar