No CrossRef data available.
Published online by Cambridge University Press: 04 October 2017
Let 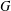 $G$ be a simple connected graph with
$G$ be a simple connected graph with  $n$ vertices and
$n$ vertices and 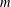 $m$ edges and
$m$ edges and 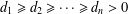 $d_{1}\geq d_{2}\geq \cdots \geq d_{n}>0$ its sequence of vertex degrees. If
$d_{1}\geq d_{2}\geq \cdots \geq d_{n}>0$ its sequence of vertex degrees. If 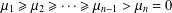 $\unicode[STIX]{x1D707}_{1}\geq \unicode[STIX]{x1D707}_{2}\geq \cdots \geq \unicode[STIX]{x1D707}_{n-1}>\unicode[STIX]{x1D707}_{n}=0$ are the Laplacian eigenvalues of
$\unicode[STIX]{x1D707}_{1}\geq \unicode[STIX]{x1D707}_{2}\geq \cdots \geq \unicode[STIX]{x1D707}_{n-1}>\unicode[STIX]{x1D707}_{n}=0$ are the Laplacian eigenvalues of 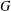 $G$, then the Kirchhoff index of
$G$, then the Kirchhoff index of 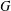 $G$ is
$G$ is 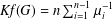 $\mathit{Kf}(G)=n\sum _{i=1}^{n-1}\unicode[STIX]{x1D707}_{i}^{-1}$. We prove some new lower bounds for
$\mathit{Kf}(G)=n\sum _{i=1}^{n-1}\unicode[STIX]{x1D707}_{i}^{-1}$. We prove some new lower bounds for 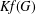 $\mathit{Kf}(G)$ in terms of some of the parameters
$\mathit{Kf}(G)$ in terms of some of the parameters 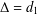 $\unicode[STIX]{x1D6E5}=d_{1}$,
$\unicode[STIX]{x1D6E5}=d_{1}$, 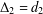 $\unicode[STIX]{x1D6E5}_{2}=d_{2}$,
$\unicode[STIX]{x1D6E5}_{2}=d_{2}$, 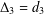 $\unicode[STIX]{x1D6E5}_{3}=d_{3}$,
$\unicode[STIX]{x1D6E5}_{3}=d_{3}$, 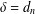 $\unicode[STIX]{x1D6FF}=d_{n}$,
$\unicode[STIX]{x1D6FF}=d_{n}$, 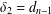 $\unicode[STIX]{x1D6FF}_{2}=d_{n-1}$ and the topological index
$\unicode[STIX]{x1D6FF}_{2}=d_{n-1}$ and the topological index 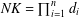 $\mathit{NK}=\prod _{i=1}^{n}d_{i}$.
$\mathit{NK}=\prod _{i=1}^{n}d_{i}$.
This work was supported by the Serbian Ministry for Education, Science and Technological Development.