Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T12:02:12.634Z Has data issue: false hasContentIssue false
  • English
  • Français

Some fixed-point theorems on locally convex linear topological spaces

Published online by Cambridge University Press:  17 April 2009

E. Tarafdar
E. Tarafdar
Affiliation:
Department of Mathematics, University of Queensland, St Lucia, Queensland 4067.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (E, τ) be a locally convex linear Hausdorff topological space. We have proved mainly the following results.

(i) Let f be nonexpansive on a nonempty τ-sequentially complete, τ-bounded, and starshaped subset M of E and let (I-f) map τ-bounded and τ-sequentially closed subsets of M into τ-sequentially closed subsets of M. Then f has a fixed-point in M.

(ii) Let f be nonexpansive on a nonempty, τ-sequentially compact, and starshaped subset M of E. Then f has a fixed-point in M.

(iii) Let (E, τ) be τ-quasi-complete. Let X be a nonempty, τ-bounded, τ-closed, and convex subset of E and M be a τ-compact subset of X. Let F be a commutative family of nonexpansive mappings on X having the property that for some f1 ∈ F and for each x ∈ X, τ-closure of the set

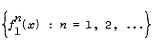
contains a point of M. Then the family F has a common fixed-point in M.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 13 , Issue 2 , October 1975 , pp. 241 - 254
Copyright
Copyright © Australian Mathematical Society 1975

References

[1]Belluce, L.P. and Kirk, W.A., “Fixed-point theorems for families of contraction mappings”, Pacific J. Math. 18 (1966), 213–217.CrossRefGoogle Scholar
[2]Day, Mahlon M., “Fixed-point theorems for compact convex sets”, Illinois J. Math. 5 (1961), 585–590.CrossRefGoogle Scholar
[3]DeMarr, Ralph, “Common fixed points for commuting contraction mappings”, Pacific J. Math. 13 (1963), 1139–1141.CrossRefGoogle Scholar
[4]Göhde, Dietrich, “Über Fixpunkte bei stetigen Selbstabbildungen mit kompakten Iterierten”, Math. Nachr. 28 (1964/1965), 45–55.CrossRefGoogle Scholar
[5]Horváth, John, Topological vector spaces and distributions, Volume I (Addison-Wesley, Reading, Massachusetts; Palo Alto; London; Don Mills, Ontario; 1966).Google Scholar
[6]Kakutani, S., “Two fixed-point theorems concerning bicompact convex sets”, Proc. Imp. Acad. Tokyo 14 (1938), 242–245.Google Scholar
[7]Köthe, Gottfried, Topological vector spaces, I (translated by Garling, D.J.H.. Die Grundlehren der mathematischen Wissenschaften, 159. Springer-Verlag, Berlin, Heidelberg, New York, 1969).Google Scholar
[8]Markov, A., “Quelques théorèmes sur les ensembles abéliens”, C.R. Acad. Sci. URSS (NS) 1 (1936), 311–313.Google Scholar
[9]Tarafdar, E., “An approach to fixed-point theorems on uniform spaces”, Trans. Amer. Math. Soc. 191 (1974), 209–225.CrossRefGoogle Scholar
[10]Taylor, W.W., “Fixed-point theorems for nonexpansive mappings in linear topological spaces”, J. Math. Anal. Appl. 40 (1972), 164–173.CrossRefGoogle Scholar