Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-05-02T01:17:56.972Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME COUNTING QUESTIONS FOR MATRIX PRODUCTS

Part of: Basic linear algebra Polynomials and matrices

Published online by Cambridge University Press:  09 October 2023

MUHAMMAD AFIFURRAHMAN Open the ORCID record for MUHAMMAD AFIFURRAHMAN [Opens in a new window]
MUHAMMAD AFIFURRAHMAN*
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney NSW 2052, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

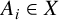Given a set X of $n\times n$ matrices and a positive integer m, we consider the problem of estimating the cardinalities of the product sets $A_1 \cdots A_m$, where $A_i\in X$. When 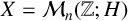$X={\mathcal M}_n(\mathbb {Z};H)$, the set of $n\times n$ matrices with integer elements of size at most H, we give several bounds on the cardinalities of the product sets and solution sets of related equations such as 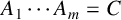$A_1 \cdots A_m=C$ and 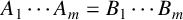$A_1 \cdots A_m=B_1 \cdots B_m$. We also consider the case where X is the subset of matrices in 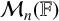${\mathcal M}_n(\mathbb {F})$, where 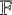$\mathbb {F}$ is a field with bounded rank 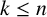$k\leq n$. In this case, we completely classify the related product set.

Keywords

matrixmatrix equationinteger matrixmatrix product

MSC classification

Primary: 11C20: Matrices, determinants
Secondary: 15A24: Matrix equations and identities
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 1 , August 2024 , pp. 32 - 43
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author is supported by an UNSW Tuition Fee Scholarship and Australian Research Council Grant DP200100355.

References

Ahmadi, O. and Shparlinski, I. E., ‘Distribution of matrices with restricted entries over finite fields’, Indag. Math. (N.S.) 18 (2007), 327–337.CrossRefGoogle Scholar
Demiroğlu-Karabulut, Y., Koh, D., Pham, T., Shen, C.-Y. and Vinh Le, A., ‘Expanding phenomena over matrix rings’, Forum Math. 31 (2019), 951–970.CrossRefGoogle Scholar
Duke, W., Rudnick, Z. and Sarnak, P., ‘Density of integer points on affine homogeneous varieties’, Duke Math. J. 71 (1993), 143–79.CrossRefGoogle Scholar
El-Baz, D., Lee, M. and Strömbergsson, A., ‘Effective equidistribution of primitive rational points on expanding horospheres’, Preprint, 2023, arXiv:2212.07408.CrossRefGoogle Scholar
Erdős, P.. ‘An asymptotic inequality in the theory of numbers’, Vestnik Leningrad. Univ. 15 (1960), 41–49.Google Scholar
Ferguson, R., Hoffman, C., Luca, F., Ostafe, A. and Shparlinski, I. E., ‘Some additive combinatorics problems in matrix rings’, Rev. Mat. Complut. 23 (2010), 501–513.CrossRefGoogle Scholar
Fisher, S. D., ‘Classroom notes: matrices over a finite field’, Amer. Math. Monthly 73 (1966), 639–641.Google Scholar
Ford, K., ‘The distribution of integers with a divisor in a given interval’, Ann. of Math. (2) 168 (2008), 367–433.CrossRefGoogle Scholar
Helfgott, H. A., ‘Growth and generation in $\mathrm{SL}_2(\mathbb{Z}/ p\mathbb{Z})$ ’, Ann. of Math. (2) 167 (2008), 601–623.CrossRefGoogle Scholar
Helfgott, H. A., ‘Growth in $\mathrm{SL}_3(\mathbb{Z}/ p\mathbb{Z})$ ’, J. Eur. Math. Soc. (JEMS) 13 (2011), 761–851.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
Katznelson, Y. R., ‘Singular matrices and a uniform bound for congruence groups of ${\mathrm{SL}}_n(\mathbb{Z})$ ’, Duke Math. J. 69 (1993), 121–136.CrossRefGoogle Scholar
Katznelson, Y. R., ‘Integral matrices of fixed rank’, Proc. Amer. Math. Soc. 120 (1994), 667–675.CrossRefGoogle Scholar
Koukoulopoulos, D., ‘Localized factorizations of integers’, Proc. Lond. Math. Soc. (3) 101 (2010), 392–426.CrossRefGoogle Scholar
Mohammadi, A., Pham, T. and Wang, Y., ‘An energy decomposition theorem for matrices and related questions’, Canad. Math. Bull., to appear. Published online (15 May 2023).CrossRefGoogle Scholar
Nguyen, T. and Vinh, L. A., ‘A point-plane incidence theorem in matrix rings’, Discrete Appl. Math. 322 (2022), 166–170.CrossRefGoogle Scholar
Ostafe, A. and Shparlinski, I. E., ‘Integer matrices with a given characteristic polynomial and multiplicative dependence of matrices’, Preprint, 2023, arXiv:2203.03880.Google Scholar
Shparlinski, I. E., ‘Some counting questions for matrices with restricted entries’, Linear Algebra Appl. 432 (2010), 155–160.CrossRefGoogle Scholar
Van The, N. and Vinh, L. A., ‘Expanding phenomena over higher dimensional matrix rings’, J. Number Theory 216 (2020), 174–91.Google Scholar
Xie, C. and Ge, G., ‘Some sum-product estimates in matrix rings over finite fields’, Finite Fields Appl. 79 (2022), 101997.CrossRefGoogle Scholar