Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T07:08:25.296Z Has data issue: false hasContentIssue false
  • English
  • Français

SOLVABILITY FOR A NONLINEAR FRACTIONAL DIFFERENTIAL EQUATION

Part of: Boundary value problems

Published online by Cambridge University Press:  19 June 2009

YINGXIN GUO
YINGXIN GUO*
Affiliation:
Department of Mathematics, Qufu Normal University, Qufu, Shandong 273165, PR China (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

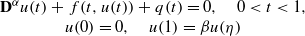In this paper, we consider the existence of nontrivial solutions for the nonlinear fractional differential equation boundary-value problem (BVP) where 1<α≤2, η∈(0,1),β∈ℝ=(−∞,+∞), βηα−1≠1, Dα is the Riemann–Liouville differential operator of order α, and f:[0,1]×ℝ→ℝ is continuous, q(t):[0,1]→[0,+∞) is Lebesgue integrable. We give some sufficient conditions for the existence of nontrivial solutions to the above boundary-value problems. Our approach is based on the Leray–Schauder nonlinear alternative. Particularly, we do not use the nonnegative assumption and monotonicity on f which was essential for the technique used in almost all existed literature.

Keywords

Caputo’s fractional derivativefractional differential equationboundary-value problemnontrivial solutionLeray–Schauder nonlinear alternative

MSC classification

Secondary: 34B15: Nonlinear boundary value problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 80 , Issue 1 , August 2009 , pp. 125 - 138
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

The authors were supported financially by the NNSF of China (10726004) and the NSF of Shandong Province of China (Q2007A02).

References

[1] Agrawal, O. P., ‘Formulation of Euler–Larange equations for fractional variational problems’, J. Math. Anal. Appl. 272 (2002), 368–379.CrossRefGoogle Scholar
[2] Bai, Z. and Lü, H., ‘Positive solutions for boundary-value problem of nonlinear fractional differential equation’, J. Math. Anal. Appl. 311 (2005), 495–505.CrossRefGoogle Scholar
[3] Deimling, K., Nonlinear Functional Analysis (Springer, Berlin, 1985).CrossRefGoogle Scholar
[4] Delbosco, D. and Rodino, L., ‘Existence and uniqueness for a nonlinear fractional differential equation’, J. Math. Appl. 204 (1996), 609–625.Google Scholar
[5] Kaufmann, E. R. and Mboumi, E., ‘Positive solutions of a boundary value problem for a nonlinear fractional differential equations’, Electron. J. Qual. Theory Differ. Equ. (3) (2008), 1–11.CrossRefGoogle Scholar
[6] Kilbas, A. A. and Trujillo, J. J., ‘Differential equations of fractional order: methods, results and problems II’, Appl. Anal. 81 (2002), 435–493.CrossRefGoogle Scholar
[7] Liu, B., ‘Positive solutions of a nonlinear three-point boundary value problem’, Comput. Math. Appl. 44 (2002), 201–211.CrossRefGoogle Scholar
[8] Nakhushev, A. M., ‘The Sturm–Liouville problem for a second order ordinary differential equation with fractional derivatives in the lower terms’, Dokl. Akad. Nauk SSSR 234 (1977), 308–311.Google Scholar
[9] Podlubny, I., Fractional Differential Equations, Mathematics in Science and Engineering, 198  (Academic Press, San Diego, 1999).Google Scholar
[10] Samko, S. G., Kilbas, A. A. and Marichev, O. I., Fractional Integral And Derivatives (Theory and Applications) (Gordon and Breach, Yverdon, 1993).Google Scholar
[11] Zhang, S-Q., ‘The existence of a positive solution for a nonlinear fractional differential equation’, J. Math. Anal. Appl. 252 (2000), 804–812.CrossRefGoogle Scholar
[12] Zhang, S-Q., ‘Existence of positive solution for some class of nonlinear fractional differential equations’, J. Math. Anal. Appl. 278(1) (2003), 136–148.CrossRefGoogle Scholar