No CrossRef data available.
Published online by Cambridge University Press: 24 May 2021
We find all integer solutions to the equation
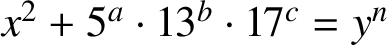 $x^2+5^a\cdot 13^b\cdot 17^c=y^n$
with
$x^2+5^a\cdot 13^b\cdot 17^c=y^n$
with
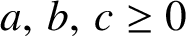 $a,\,b,\,c\geq 0$
,
$a,\,b,\,c\geq 0$
,
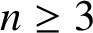 $n\geq 3$
,
$n\geq 3$
,
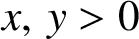 $x,\,y>0$
and
$x,\,y>0$
and
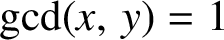 $\gcd (x,\,y)=1$
. Our proof uses a deep result about primitive divisors of Lucas sequences in combination with elementary number theory and computer search.
$\gcd (x,\,y)=1$
. Our proof uses a deep result about primitive divisors of Lucas sequences in combination with elementary number theory and computer search.
The author is partially supported by the Vietnam Institute for Advanced Study in Mathematics (VIASM) and the Vietnam National Foundation for Science and Technology Development (NAFOSTED) (grant number 101.04-2019.314).