Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-04T00:12:29.995Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth families of fibrations and analytic selections of polynomial hulls

Published online by Cambridge University Press:  17 April 2009

Miran Černe
Miran Černe
Affiliation:
University of LjubljanaIMFM Jadranska 1961 111 LjubljanaSlovenia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Constructed are strictly increasing smooth families Σt ⊆ ∂D × C2, t ∈ [0, 1], of fibrations over the unit circle with strongly pseudoconvex fibers all diffeomorphic to the ball 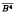such that there is no analytic selection of the polynomial hull of Σ0 and which end at the product fibration 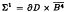. In particular these examples show that the continuity method for describing the polynomial hull of a fibration over ∂D fails even if the complex geometry of the fibers is relatively simple.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 52 , Issue 1 , August 1995 , pp. 97 - 105
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Alexander, H. and Wermer, J., ‘Polynomial hulls with convex fibers’, Math. Ann. 271 (1985), 99–109.CrossRefGoogle Scholar
[2]Černe, M., Analytic discs with boundaries in a generating CR-manifold, Ph.D. Thesis (Madison, 1994).Google Scholar
[3]Docquier, F. and Grauert, H., ‘Levisches Problem and Rungescher Satz für Teilgebiete Steinscher Mannigfaltigkeiten’, Math. Ann. 140 (1960), 94–123.CrossRefGoogle Scholar
[4]Forstnerič, F., ‘Polynomially convex hulls with piecewise smooth boundaries’, Math. Ann. 276 (1986), 97–104.CrossRefGoogle Scholar
[5]Forstnerič, F., ‘Polynomial hulls of sets fibered over the circle’, Indiana Univ. Math. J. 37 (1988), 869–889.CrossRefGoogle Scholar
[6]Helton, J.W. and Merino, O., ‘A fibered polynomial hull without an analytic selection’, Michigen Math. J. 41 (1994), 285–287.Google Scholar
[7]Slodkowski, Z., ‘Polynomial hulls with convex sections and interpolating spaces’, Proc. Amer. Math. Soc. 96 (1986), 255–260.CrossRefGoogle Scholar
[8]Slodkowski, Z., ‘Polynomial hulls in C2 and quasicircles’, Ann. Scuola Norm. Sup. Pisa Cl. Sci. 16 (1989), 367–391.Google Scholar
[9]Slodkowski, Z., ‘Polynomial hulls with convex fibers and complex geodesies’, J. Funct. Anal. 94 (1990), 156–176.CrossRefGoogle Scholar
[10]Stolzenberg, G., ‘A hull with no analytic structure’, J. Math. Mech. 12 (1963), 103–111.Google Scholar
[11]Wermer, J., ‘Polynomial convex hulls and analyticity’, Ark. Mat. 20 (1982), 129–13.CrossRefGoogle Scholar