Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-17T16:58:23.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Small zeros of quadratic L-functions

Published online by Cambridge University Press:  17 April 2009

Ali E. Özlük  and
C. Snyder
Ali E. Özlük
Affiliation:
Department of Mathematics, University of Maine, Neville Hall Orono ME 04469 0122, United States of America
C. Snyder
Affiliation:
Department of Mathematics, University of Maine, Neville Hall Orono ME 04469 0122, United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the distribution of the imaginary parts of zeros near the real axis of quadratic L-functions. More precisely, let K(s) be chosen so that |K(1/2 ± it)| is rapidly decreasing as t increases. We investigate the asymptotic behaviour of

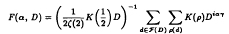
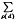as D → ∞. Here denotes the sum over the non-trivial zeros p = 1/2 + iγ of the Dirichlet L-function L(s, χd), and χd = (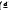) is the Kronecker symbol. The outer sum 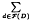is over all fundamental discriminants d that are in absolute value ≤ D. Assuming the Generalized Riemann Hypothesis, we show that for

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 47 , Issue 2 , April 1993 , pp. 307 - 319
Copyright
Copyright © Australian Mathematical Society 1993

References

[1]Ayoub, R.G., An introduction to the analytic theory of numbers 10 (Math. Surveys, Providence, R.I., 1963).Google Scholar
[2]Bellman, R., Analytic number theory, an introduction (Benjamin Cummings Pub. Co., 1980).Google Scholar
[3]Bentz, H.-J. and Pintz, J., ‘Quadratic residues and the distribution of prime numbers’, Monatshefte für Mathematik 90 (1982), 91–100.CrossRefGoogle Scholar
[4]Bentz, H.-J., ‘Discrepancies in the distribution of prime numbers’, J. Number Theory 15 (1982), 252–274.CrossRefGoogle Scholar
[5]Chebysev, P.L., ‘Lettres de M. le professeur Tchebychev á M. Fuss sur un nouveau théorème relative aux nombres premiers contenus dans les formes 4n + 1 et 4n + 3’, Bull. Classe Phys. de l'Acad. Imp. Sciences St. Petersburg 11 (1853), 208.Google Scholar
[6]Davenport, H., Multiplicative number theory, 2nd ed. (Springer-Verlag, Berlin, Heidelberg, New York, 1980).CrossRefGoogle Scholar
[7]Ellison, F. and Ellison, W., Prime numbers (John Wiley, New York, 1985).Google Scholar
[8]Montgomery, H.L. and Weinberger, P.J., ‘Notes on small class numbers’, Acta Arith. 24 (1974), 529–542.CrossRefGoogle Scholar
[9]Shanks, D., ‘Quadratic residues and the distribution of primes’, Math. Tables and other Aids to Comp. 13 (1959), 272–284.CrossRefGoogle Scholar
[10]Turán, P., On a new method of analysis and its applications (John Wiley and Sons, Inc., New York, 1984).Google Scholar
[11]Weinberger, P.J., ‘On small zeros of Dirichlet L-functions’, Math. Comp. 29 (1975), 319–328.Google Scholar