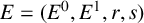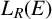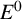1 Introduction
The Leavitt path algebra of a row-finite graph, over a field, was introduced in [Reference Abrams and Aranda Pino2, Reference Ara, Moreno and Pardo5] and has since then been successively generalised (see, for example, [Reference Abrams and Aranda Pino3, Reference Tomforde20]). The Leavitt path algebra of an arbitrary directed graph, over a unital ring, was introduced in [Reference Hazrat12]. For an account of the development of the field of Leavitt path algebras, we refer the reader to [Reference Abrams1]. Here is our first main result.
Theorem 1.1. Suppose that R is an associative unital ring and that
![]() $E=(E^0,E^1,r,s)$
is a directed graph. The Leavitt path algebra
$E=(E^0,E^1,r,s)$
is a directed graph. The Leavitt path algebra
![]() $L_R(E)$
is simple if and only if R is simple,
$L_R(E)$
is simple if and only if R is simple,
![]() $E^0$
has no nontrivial hereditary and saturated subset, and every cycle in E has an exit.
$E^0$
has no nontrivial hereditary and saturated subset, and every cycle in E has an exit.
Characterisations of simple Leavitt path algebras over fields have previously been established in [Reference Tomforde19, Theorem 6.18], [Reference Abrams and Aranda Pino3, Theorem 3.1] and [Reference Gonçalves, Öinert and Royer11, Theorem 3.5]. Theorem 1.1 generalises all of those results, and also partially generalises [Reference Tomforde20, Theorem 7.20]. Our second main result, stated below, completely describes the centre of a simple Leavitt path algebra. It generalises [Reference Aranda Pino and Crow6, Theorem 4.2] from the case where R is a field and E is a row-finite graph.
Theorem 1.2. Suppose that R is an associative unital ring and that
![]() $E=(E^0,E^1,r,s)$
is a directed graph. Furthermore, suppose that
$E=(E^0,E^1,r,s)$
is a directed graph. Furthermore, suppose that
![]() $L_R(E)$
is a simple Leavitt path algebra. The following assertions hold.
$L_R(E)$
is a simple Leavitt path algebra. The following assertions hold.
-
(a) If
 $L_R(E)$
is not unital, then
$L_R(E)$
is not unital, then
 $Z(L_R(E)) = \{0\}$
.
$Z(L_R(E)) = \{0\}$
. -
(b) If
 $L_R(E)$
is unital, then
$L_R(E)$
is unital, then
 $Z(L_R(E)) = Z(R) \cdot 1_{L_R(E)}$
.
$Z(L_R(E)) = Z(R) \cdot 1_{L_R(E)}$
.
Whereas earlier proofs of Theorems 1.1 and 1.2 (when R is a field) use ad hoc arguments, specifically designed for graph algebras, we use the general theory of graded rings to obtain our results. This makes our proofs shorter and, we believe, clearer. Indeed, we show that
![]() $L_R(E)$
is graded simple if and only if R is simple and
$L_R(E)$
is graded simple if and only if R is simple and
![]() $E^0$
has no nontrivial hereditary and saturated subset (see Proposition 3.6). We also show that every cycle in E has an exit if and only if the centre of each corner subring of
$E^0$
has no nontrivial hereditary and saturated subset (see Proposition 3.6). We also show that every cycle in E has an exit if and only if the centre of each corner subring of
![]() $L_R(E)$
at a vertex has degree zero (see Proposition 3.14).
$L_R(E)$
at a vertex has degree zero (see Proposition 3.14).
We point out that there are various generalisations of Leavitt path algebras in the literature (see, for example, [Reference Abrams1, Section 5] and [Reference Clark, Farthing, Sims and Tomforde9, Reference Steinberg18]). A simplicity result for Steinberg algebras was obtained in [Reference Clark and Edie-Michell8], and when translated to Leavitt path algebras, one recovers Theorem 1.1 in the special case where R is a commutative unital ring. Note that [Reference Aranda Pino and Crow6, Theorem 4.2] was generalised to Kumjian–Pask algebras in [Reference Brown and an Huef7], and in [Reference Clark, Martín Barquero, Martín González and Siles Molina10], Steinberg algebra techniques were used to give a complete description of the centre of a general (not necessarily simple) Leavitt path algebra
![]() $L_R(E)$
, where R is a commutative unital ring.
$L_R(E)$
, where R is a commutative unital ring.
2 Simple
 $\mathbb {Z}$
-graded rings
$\mathbb {Z}$
-graded rings
Let
![]() $\mathbb {Z}$
denote the rational integers and write
$\mathbb {Z}$
denote the rational integers and write
![]() $\mathbb {N} := \{ 1,2,3,\ldots \}$
. Suppose that S is a ring. By this, we mean that S is associative but not necessarily unital. If S is unital, then we let
$\mathbb {N} := \{ 1,2,3,\ldots \}$
. Suppose that S is a ring. By this, we mean that S is associative but not necessarily unital. If S is unital, then we let
![]() $1_S$
denote the multiplicative identity of S. Furthermore, we let
$1_S$
denote the multiplicative identity of S. Furthermore, we let
![]() $Z(S)$
denote the centre of S, that is, the set of all
$Z(S)$
denote the centre of S, that is, the set of all
![]() $s \in S$
satisfying
$s \in S$
satisfying
![]() $st = ts$
for every
$st = ts$
for every
![]() $t \in S$
. Recall that S is said to be
$t \in S$
. Recall that S is said to be
![]() $\mathbb {Z}$
-graded if, for each
$\mathbb {Z}$
-graded if, for each
![]() $n \in \mathbb {Z}$
, there is an additive subgroup
$n \in \mathbb {Z}$
, there is an additive subgroup
![]() $S_n$
of S such that
$S_n$
of S such that
![]() $S = \oplus _{n\in \mathbb {Z}} S_n$
and
$S = \oplus _{n\in \mathbb {Z}} S_n$
and
![]() $S_n S_m \subseteq S_{n+m}$
, for all
$S_n S_m \subseteq S_{n+m}$
, for all
![]() $n,m\in \mathbb {Z}$
. In that case, each element
$n,m\in \mathbb {Z}$
. In that case, each element
![]() $s\in S$
may be written as
$s\in S$
may be written as
![]() $s=\sum _{n\in \mathbb {Z}} s_n$
, where
$s=\sum _{n\in \mathbb {Z}} s_n$
, where
![]() $s_n \in S_n$
is zero for all but finitely many
$s_n \in S_n$
is zero for all but finitely many
![]() $n\in \mathbb {Z}$
. The support of s is defined as the finite set
$n\in \mathbb {Z}$
. The support of s is defined as the finite set
![]() $\operatorname {\mathrm {Supp}}(s):=\{n\in \mathbb {Z} \mid s_n \neq 0\}$
. An ideal I of a
$\operatorname {\mathrm {Supp}}(s):=\{n\in \mathbb {Z} \mid s_n \neq 0\}$
. An ideal I of a
![]() $\mathbb {Z}$
-graded ring S is said to be graded if
$\mathbb {Z}$
-graded ring S is said to be graded if
![]() $I=\oplus _{n\in \mathbb {Z}} (I \cap S_n)$
. If
$I=\oplus _{n\in \mathbb {Z}} (I \cap S_n)$
. If
![]() $\{0\}$
and S are the only graded ideals of S, then S is said to be graded simple.
$\{0\}$
and S are the only graded ideals of S, then S is said to be graded simple.
We recall some properties of graded rings.
Lemma 2.1. Suppose that S is a unital
![]() $\mathbb {Z}$
-graded ring.
$\mathbb {Z}$
-graded ring.
-
(a) The ring
 $Z(S)$
is
$Z(S)$
is
 $\mathbb {Z}$
-graded with respect to the grading
$\mathbb {Z}$
-graded with respect to the grading
 $Z(S)_n$
which is defined by
$Z(S)_n$
which is defined by
 $Z(S)_n := Z(S) \cap S_n$
for
$Z(S)_n := Z(S) \cap S_n$
for
 $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
. -
(b) If S is a field, then
 $S = S_0$
.
$S = S_0$
.
Proof. Item (a) is [Reference Năstăsescu and van Oystaeyen15, page 15, Exercise 8] and item (b) is [Reference Năstăsescu and van Oystaeyen15, Remark 1.3.10].
Next, we state a special case of [Reference Nystedt and Öinert17, Theorem 1.2] and [Reference Jespers13, Theorem 5]. For the convenience of the reader, we include a shortened version of the proof from these sources adapted to the situation at hand.
Proposition 2.2. Suppose that S is a unital
![]() $\mathbb {Z}$
-graded ring. Then, the following assertions are equivalent:
$\mathbb {Z}$
-graded ring. Then, the following assertions are equivalent:
-
(i) S is simple;
-
(ii) S is graded simple and
 $Z(S)$
is a field;
$Z(S)$
is a field; -
(iii) S is graded simple and
 $Z(S) \subseteq S_0$
.
$Z(S) \subseteq S_0$
.
Proof. (i)
![]() $\Rightarrow $
(ii) is clear and (ii)
$\Rightarrow $
(ii) is clear and (ii)
![]() $\Rightarrow $
(iii) follows from Lemma 2.1. Now we show that (iii)
$\Rightarrow $
(iii) follows from Lemma 2.1. Now we show that (iii)
![]() $\Rightarrow $
(i). Suppose that S is graded simple and that
$\Rightarrow $
(i). Suppose that S is graded simple and that
![]() $Z(S) \subseteq S_0$
. Let I be a nonzero ideal of S. We wish to show that
$Z(S) \subseteq S_0$
. Let I be a nonzero ideal of S. We wish to show that
![]() $1_S \in I$
. Amongst all nonzero elements of I, choose s such that
$1_S \in I$
. Amongst all nonzero elements of I, choose s such that
![]() $|\!\operatorname {\mathrm {Supp}}(s)|$
is minimal. Take
$|\!\operatorname {\mathrm {Supp}}(s)|$
is minimal. Take
![]() $m \in \operatorname {\mathrm {Supp}}(s)$
. Since S is graded simple, there are
$m \in \operatorname {\mathrm {Supp}}(s)$
. Since S is graded simple, there are
![]() $n \in \mathbb {N}$
and homogeneous elements
$n \in \mathbb {N}$
and homogeneous elements
![]() $p_1,\ldots ,p_n,q_1,\ldots ,q_n \in S$
, such that
$p_1,\ldots ,p_n,q_1,\ldots ,q_n \in S$
, such that
![]() $\sum _{i=1}^n p_i s_m q_i = 1_S$
and
$\sum _{i=1}^n p_i s_m q_i = 1_S$
and
![]() $p_i s_m q_i \in S_0 \setminus \{0\}$
for every
$p_i s_m q_i \in S_0 \setminus \{0\}$
for every
![]() $i\in \{1,\ldots ,n\}$
. Write
$i\in \{1,\ldots ,n\}$
. Write
![]() $t := \sum _{i=1}^n p_i s q_i$
. Note that
$t := \sum _{i=1}^n p_i s q_i$
. Note that
![]() $t \in I$
,
$t \in I$
,
![]() $t_0 = 1_S$
and
$t_0 = 1_S$
and
![]() $|\!\operatorname {\mathrm {Supp}}(t)| \leq |\!\operatorname {\mathrm {Supp}}(s)|$
. Take
$|\!\operatorname {\mathrm {Supp}}(t)| \leq |\!\operatorname {\mathrm {Supp}}(s)|$
. Take
![]() $z \in \mathbb {Z}$
and
$z \in \mathbb {Z}$
and
![]() $x \in S_z$
. Then,
$x \in S_z$
. Then,
![]() $tx-xt \in I$
and, since
$tx-xt \in I$
and, since
![]() $t_0 = 1_S$
, it follows that
$t_0 = 1_S$
, it follows that
![]() $|\!\operatorname {\mathrm {Supp}}(tx - xt)| < |\!\operatorname {\mathrm {Supp}}(t)|$
. By the assumptions on s, we get
$|\!\operatorname {\mathrm {Supp}}(tx - xt)| < |\!\operatorname {\mathrm {Supp}}(t)|$
. By the assumptions on s, we get
![]() $|\!\operatorname {\mathrm {Supp}}(tx - xt)| = 0$
and hence
$|\!\operatorname {\mathrm {Supp}}(tx - xt)| = 0$
and hence
![]() $xt = tx$
. Thus,
$xt = tx$
. Thus,
![]() $t \in Z(S) \subseteq S_0$
. We conclude that
$t \in Z(S) \subseteq S_0$
. We conclude that
![]() $1_S = t_0 = t \in I$
.
$1_S = t_0 = t \in I$
.
Let S be a ring. Recall from [Reference Ánh and Márki4] (see also [Reference Nystedt16]) that a set U of idempotents in S is called a set of local units for S if for every
![]() $n \in \mathbb {N}$
and all
$n \in \mathbb {N}$
and all
![]() $s_1,\ldots ,s_n \in S$
, there is some
$s_1,\ldots ,s_n \in S$
, there is some
![]() $e \in U$
such that
$e \in U$
such that
![]() $e s_i = s_i e = s_i$
for every
$e s_i = s_i e = s_i$
for every
![]() $i \in \{1,\ldots ,n\}$
.
$i \in \{1,\ldots ,n\}$
.
Remark 2.3. Suppose that S is a
![]() $\mathbb {Z}$
-graded ring. If
$\mathbb {Z}$
-graded ring. If
![]() $e\in S_0$
is an idempotent, then the corner subring
$e\in S_0$
is an idempotent, then the corner subring
![]() $eSe$
inherits a natural
$eSe$
inherits a natural
![]() $\mathbb {Z}$
-grading defined by
$\mathbb {Z}$
-grading defined by
![]() $(eSe)_n:= e S_n e$
for
$(eSe)_n:= e S_n e$
for
![]() $n\in \mathbb {Z}$
.
$n\in \mathbb {Z}$
.
For future reference, we recall the following two results.
Proposition 2.4. Suppose that S is a
![]() $\mathbb {Z}$
-graded ring equipped with a set of local units
$\mathbb {Z}$
-graded ring equipped with a set of local units
![]() $U \subseteq S_0$
. Then, S is (graded) simple if and only if, for every
$U \subseteq S_0$
. Then, S is (graded) simple if and only if, for every
![]() $f \in U$
, the ring
$f \in U$
, the ring
![]() $f S f$
is (graded) simple.
$f S f$
is (graded) simple.
Proof. First we show the ‘only if’ statement. Suppose that S is (graded) simple and that
![]() $f \in U$
. Let J be a nonzero (graded) ideal of
$f \in U$
. Let J be a nonzero (graded) ideal of
![]() $f S f$
. By (graded) simplicity of S, it follows that
$f S f$
. By (graded) simplicity of S, it follows that
![]() $SJS = S$
. Thus,
$SJS = S$
. Thus,
![]() $fSf = fSJSf = (fSf)J(fSf) \subseteq J$
and hence
$fSf = fSJSf = (fSf)J(fSf) \subseteq J$
and hence
![]() $J = fSf$
. Next, we show the ‘if’ statement. Suppose that
$J = fSf$
. Next, we show the ‘if’ statement. Suppose that
![]() $fSf$
is (graded) simple for every
$fSf$
is (graded) simple for every
![]() $f \in U$
. Let I be a nonzero (graded) ideal of S. Take a nonzero (homogeneous)
$f \in U$
. Let I be a nonzero (graded) ideal of S. Take a nonzero (homogeneous)
![]() $x \in S$
. Take a nonzero (homogeneous)
$x \in S$
. Take a nonzero (homogeneous)
![]() $y \in I$
and
$y \in I$
and
![]() $f \in U$
with
$f \in U$
with
![]() $fx = xf = x$
and
$fx = xf = x$
and
![]() $fy = yf = y$
. By (graded) simplicity of
$fy = yf = y$
. By (graded) simplicity of
![]() $fSf$
, it follows that
$fSf$
, it follows that
![]() $I \supseteq f SyS f = fSf \ni x$
. Thus,
$I \supseteq f SyS f = fSf \ni x$
. Thus,
![]() $I = S$
.
$I = S$
.
Proposition 2.5. Suppose that S is a
![]() $\mathbb {Z}$
-graded ring equipped with a set of local units and that
$\mathbb {Z}$
-graded ring equipped with a set of local units and that
![]() $f \in S_0$
is a nonzero idempotent. If S is graded simple and
$f \in S_0$
is a nonzero idempotent. If S is graded simple and
![]() $f S f$
is simple, then S is simple.
$f S f$
is simple, then S is simple.
Proof. Suppose that S is graded simple and that
![]() $f S f$
is simple. Let I be a nonzero ideal of S. Take a nonzero
$f S f$
is simple. Let I be a nonzero ideal of S. Take a nonzero
![]() $s \in I$
and write
$s \in I$
and write
![]() $s = \sum _{n \in \operatorname {\mathrm {Supp}}(s)} s_n$
. Fix
$s = \sum _{n \in \operatorname {\mathrm {Supp}}(s)} s_n$
. Fix
![]() $m \in \operatorname {\mathrm {Supp}}(s)$
and define
$m \in \operatorname {\mathrm {Supp}}(s)$
and define
![]() $J := S s_m S$
. Then, J is a nonzero graded ideal of S. By graded simplicity of S, it follows that
$J := S s_m S$
. Then, J is a nonzero graded ideal of S. By graded simplicity of S, it follows that
![]() $J = S$
and, in particular, that
$J = S$
and, in particular, that
![]() $f \in J$
. Note that
$f \in J$
. Note that
![]() $f \in fJf$
. Since
$f \in fJf$
. Since
![]() $f \neq 0$
, it follows that there exist nonzero homogeneous
$f \neq 0$
, it follows that there exist nonzero homogeneous
![]() $y,z \in S$
such that
$y,z \in S$
such that
![]() $fy s_m zf$
is nonzero and
$fy s_m zf$
is nonzero and
![]() $\deg (y)+\deg (z) = -m$
. Now, define
$\deg (y)+\deg (z) = -m$
. Now, define
![]() $s' := fy s zf$
. By the construction of
$s' := fy s zf$
. By the construction of
![]() $s'$
, it follows that
$s'$
, it follows that
![]() $s' \in I \cap fSf$
and that
$s' \in I \cap fSf$
and that
![]() $s'$
is nonzero. In particular,
$s'$
is nonzero. In particular,
![]() $I \cap fSf \neq \{ 0 \}$
. Hence, by simplicity of
$I \cap fSf \neq \{ 0 \}$
. Hence, by simplicity of
![]() $fSf$
, we see that
$fSf$
, we see that
![]() $I \cap fSf = fSf$
. Thus,
$I \cap fSf = fSf$
. Thus,
![]() $f \in I$
. Note that
$f \in I$
. Note that
![]() $SfS$
is a nonzero graded ideal of S. Hence, by graded simplicity of S, we have
$SfS$
is a nonzero graded ideal of S. Hence, by graded simplicity of S, we have
![]() $I \supseteq SfS = S$
. This shows that
$I \supseteq SfS = S$
. This shows that
![]() $I = S$
.
$I = S$
.
3 Simple Leavitt path algebras
Let R be an associative unital ring and let
![]() $E = (E^0,E^1,r,s)$
be a directed graph. Recall that r (range) and s (source) are maps
$E = (E^0,E^1,r,s)$
be a directed graph. Recall that r (range) and s (source) are maps
![]() $E^1 \to E^0$
. The elements of
$E^1 \to E^0$
. The elements of
![]() $E^0$
are called vertices and the elements of
$E^0$
are called vertices and the elements of
![]() $E^1$
are called edges. The elements of
$E^1$
are called edges. The elements of
![]() $E^1$
are called real edges, while for
$E^1$
are called real edges, while for
![]() $f\in E^1$
, we call
$f\in E^1$
, we call
![]() $f^*$
a ghost edge. The set
$f^*$
a ghost edge. The set
![]() $\{f^* \mid f \in E^1\}$
will be denoted by
$\{f^* \mid f \in E^1\}$
will be denoted by
![]() $(E^1)^*$
. A path
$(E^1)^*$
. A path
![]() $\mu $
in E is a sequence of edges
$\mu $
in E is a sequence of edges
![]() $\mu = \mu _1 \ldots \mu _n$
such that
$\mu = \mu _1 \ldots \mu _n$
such that
![]() $r(\mu _i)=s(\mu _{i+1})$
for
$r(\mu _i)=s(\mu _{i+1})$
for
![]() $i\in \{1,\ldots ,n-1\}$
. In that case,
$i\in \{1,\ldots ,n-1\}$
. In that case,
![]() $s(\mu ):=s(\mu _1)$
is the source of
$s(\mu ):=s(\mu _1)$
is the source of
![]() $\mu $
,
$\mu $
,
![]() $r(\mu ):=r(\mu _n)$
is the range of
$r(\mu ):=r(\mu _n)$
is the range of
![]() $\mu $
and
$\mu $
and
![]() $|\mu |:=n$
is the length of
$|\mu |:=n$
is the length of
![]() $\mu $
. If
$\mu $
. If
![]() $\mu =\mu _1\ldots \mu _n$
is a (real) path in E, then we let
$\mu =\mu _1\ldots \mu _n$
is a (real) path in E, then we let
![]() $\mu ^*:=\mu _n^*\ldots \mu _1^*$
denote the corresponding ghost path. For any vertex
$\mu ^*:=\mu _n^*\ldots \mu _1^*$
denote the corresponding ghost path. For any vertex
![]() $v \in E^0$
, we put
$v \in E^0$
, we put
![]() $s(v):=v$
and
$s(v):=v$
and
![]() $r(v):=v$
. We let
$r(v):=v$
. We let
![]() $r(f^*)$
denote
$r(f^*)$
denote
![]() $s(f)$
and we let
$s(f)$
and we let
![]() $s(f^*)$
denote
$s(f^*)$
denote
![]() $r(f)$
. For
$r(f)$
. For
![]() $n \geq 2$
, we define
$n \geq 2$
, we define
![]() $E^n$
to be the set of paths of length n and
$E^n$
to be the set of paths of length n and
![]() $E^* := \bigcup _{n\geq 0} E^n$
the set of all finite paths.
$E^* := \bigcup _{n\geq 0} E^n$
the set of all finite paths.
Following Hazrat [Reference Hazrat12], we make the following definition.
Definition 3.1. The Leavitt path algebra of E with coefficients in R, denoted by
![]() $L_R(E)$
, is the algebra generated by the sets
$L_R(E)$
, is the algebra generated by the sets
![]() $\{v \mid v\in E^0\}$
,
$\{v \mid v\in E^0\}$
,
![]() $\{f \mid f\in E^1\}$
and
$\{f \mid f\in E^1\}$
and
![]() $\{f^* \mid f\in E^1\}$
with the coefficients in R, subject to the relations:
$\{f^* \mid f\in E^1\}$
with the coefficients in R, subject to the relations:
-
(1)
 $uv = \delta _{u,v} v$
for all
$uv = \delta _{u,v} v$
for all
 $u,v \in E^0$
;
$u,v \in E^0$
; -
(2)
 $s(f)f=fr(f)=f$
and
$s(f)f=fr(f)=f$
and
 $r(f)f^*=f^*s(f)=f^*$
for all
$r(f)f^*=f^*s(f)=f^*$
for all
 $f\in E^1$
;
$f\in E^1$
; -
(3)
 $f^*f'=\delta _{f,f'} r(f)$
for all
$f^*f'=\delta _{f,f'} r(f)$
for all
 $f,f'\in E^1$
;
$f,f'\in E^1$
; -
(4)
 $\sum _{f\in E^1, s(f)=v} ff^* = v$
for every
$\sum _{f\in E^1, s(f)=v} ff^* = v$
for every
 $v\in E^0$
for which
$v\in E^0$
for which
 $s^{-1}(v)$
is nonempty and finite.
$s^{-1}(v)$
is nonempty and finite.
Here, elements of the ring R commute with the generators.
Remark 3.2. (a) The Leavitt path algebra
![]() $L_R(E)$
carries a natural
$L_R(E)$
carries a natural
![]() $\mathbb {Z}$
-grading. Indeed, put
$\mathbb {Z}$
-grading. Indeed, put
![]() $\deg (v):=0$
for each
$\deg (v):=0$
for each
![]() $v\in E^0$
. For each
$v\in E^0$
. For each
![]() $f\in E^1$
, we put
$f\in E^1$
, we put
![]() $\deg (f):=1$
and
$\deg (f):=1$
and
![]() $\deg (f^*):=-1$
. By assigning degrees to the generators in this way, we obtain a
$\deg (f^*):=-1$
. By assigning degrees to the generators in this way, we obtain a
![]() $\mathbb {Z}$
-grading on the free algebra
$\mathbb {Z}$
-grading on the free algebra
![]() $F_R(E) = R \langle v, f, f^* \mid v \in E^0, f \in E^1 \rangle $
. Moreover, the ideal coming from relations (1)–(4) in Definition 3.1 is graded. Using this, it is easy to see that the natural
$F_R(E) = R \langle v, f, f^* \mid v \in E^0, f \in E^1 \rangle $
. Moreover, the ideal coming from relations (1)–(4) in Definition 3.1 is graded. Using this, it is easy to see that the natural
![]() $\mathbb {Z}$
-grading on
$\mathbb {Z}$
-grading on
![]() $F_R(E)$
carries over to a
$F_R(E)$
carries over to a
![]() $\mathbb {Z}$
-grading on the quotient algebra
$\mathbb {Z}$
-grading on the quotient algebra
![]() $L_R(E)$
.
$L_R(E)$
.
(b) The set
![]() $\{\sum _{v\in F} v \mid F \text { is a finite subset of } E^0\}$
is a set of local units for
$\{\sum _{v\in F} v \mid F \text { is a finite subset of } E^0\}$
is a set of local units for
![]() $L_R(E)$
. If
$L_R(E)$
. If
![]() $E^0$
is finite, then
$E^0$
is finite, then
![]() $L_R(E)$
is unital and
$L_R(E)$
is unital and
![]() $1_{L_R(E)}=\sum _{v\in E^0} v$
.
$1_{L_R(E)}=\sum _{v\in E^0} v$
.
(c) Motivated by Definition 3.1(2), for
![]() $u\in E^0$
, we write
$u\in E^0$
, we write
![]() $u^*:=u$
.
$u^*:=u$
.
Definition 3.3. Let
![]() $E=(E^0,E^1,r,s)$
be a directed graph. A subset
$E=(E^0,E^1,r,s)$
be a directed graph. A subset
![]() $H \subseteq E^0$
is said to be hereditary if
$H \subseteq E^0$
is said to be hereditary if
![]() $s(f) \in H$
implies
$s(f) \in H$
implies
![]() $r(f) \in H$
for any
$r(f) \in H$
for any
![]() $f\in E^1$
. A hereditary subset
$f\in E^1$
. A hereditary subset
![]() $H \subseteq E^0$
is called saturated if
$H \subseteq E^0$
is called saturated if
![]() $\{r(f) \in H \mid f \in E^1 \text { and } s(f)=v \} \subseteq H$
implies
$\{r(f) \in H \mid f \in E^1 \text { and } s(f)=v \} \subseteq H$
implies
![]() $v\in H$
whenever
$v\in H$
whenever
![]() $v\in E^0$
satisfies
$v\in E^0$
satisfies
![]() $0 < |s^{-1}(v)| < \infty $
.
$0 < |s^{-1}(v)| < \infty $
.
Remark 3.4. Note that
![]() $\varnothing $
and
$\varnothing $
and
![]() $E^0$
are always hereditary and saturated subsets of
$E^0$
are always hereditary and saturated subsets of
![]() $E^0$
. They are referred to as trivial.
$E^0$
. They are referred to as trivial.
Lemma 3.5. Every element in
![]() $E^0 \cup E^1 \cup (E^1)^*$
is nonzero in
$E^0 \cup E^1 \cup (E^1)^*$
is nonzero in
![]() $L_R(E)$
, and the set of real (respectively ghost) paths is linearly independent in the left R-module
$L_R(E)$
, and the set of real (respectively ghost) paths is linearly independent in the left R-module
![]() $L_R(E)$
and in the right R-module
$L_R(E)$
and in the right R-module
![]() $L_R(E)$
.
$L_R(E)$
.
Proof. The proof of [Reference Tomforde20, Proposition 4.9] immediately carries over to the case where R is a noncommutative unital ring. The same holds for the proof of [Reference Tomforde20, Proposition 3.4] in case
![]() $E^0$
and
$E^0$
and
![]() $E^1$
are countable sets. Otherwise, the proof may be adapted by taking
$E^1$
are countable sets. Otherwise, the proof may be adapted by taking
![]() $\aleph $
to be an infinite cardinal at least as large as
$\aleph $
to be an infinite cardinal at least as large as
![]() $\text {card}(E^0 \cup E^1)$
and defining
$\text {card}(E^0 \cup E^1)$
and defining
![]() $Z:=\oplus _{\aleph } R$
(with the notation of [Reference Tomforde20, Proposition 3.4]).
$Z:=\oplus _{\aleph } R$
(with the notation of [Reference Tomforde20, Proposition 3.4]).
Proposition 3.6. The Leavitt path algebra
![]() $L_R(E)$
is graded simple if and only if R is simple and
$L_R(E)$
is graded simple if and only if R is simple and
![]() $E^0$
has no nontrivial hereditary and saturated subset.
$E^0$
has no nontrivial hereditary and saturated subset.
Proof. First we show the ‘if’ statement. Suppose that R is simple and that
![]() $E^0$
has no nontrivial hereditary and saturated subset. Let I be a nonzero graded ideal of
$E^0$
has no nontrivial hereditary and saturated subset. Let I be a nonzero graded ideal of
![]() $L_R(E)$
. Consider the set
$L_R(E)$
. Consider the set
![]() $H_I := \{ v \in E^0 \mid k v \in I \text { for some nonzero } k \in R \}$
. By the same argument as in [Reference Tomforde20, Lemma 5.1],
$H_I := \{ v \in E^0 \mid k v \in I \text { for some nonzero } k \in R \}$
. By the same argument as in [Reference Tomforde20, Lemma 5.1],
![]() $H_I$
is nonempty. Furthermore, since R is simple, it follows that
$H_I$
is nonempty. Furthermore, since R is simple, it follows that
![]() $H_I = \{ v \in E^0 \mid v \in I \}$
. We wish to show that
$H_I = \{ v \in E^0 \mid v \in I \}$
. We wish to show that
![]() $H_I$
is hereditary and saturated. To this end, take
$H_I$
is hereditary and saturated. To this end, take
![]() $v\in H_I$
. Suppose that
$v\in H_I$
. Suppose that
![]() $e \in E^1$
with
$e \in E^1$
with
![]() $s(e) = v$
. Then,
$s(e) = v$
. Then,
![]() $r(e) = e^* e = e^* v e \in ~I$
. Thus,
$r(e) = e^* e = e^* v e \in ~I$
. Thus,
![]() $H_I$
is hereditary. Now, take
$H_I$
is hereditary. Now, take
![]() $v\in E^0$
such that
$v\in E^0$
such that
![]() $0 < |s^{-1}(v)| < \infty $
, and suppose that
$0 < |s^{-1}(v)| < \infty $
, and suppose that
![]() $r(s^{-1}(v)) \subseteq H_I$
. For each
$r(s^{-1}(v)) \subseteq H_I$
. For each
![]() $e \in s^{-1}(v)$
, we have
$e \in s^{-1}(v)$
, we have
![]() $r(e) \in H_I$
and hence
$r(e) \in H_I$
and hence
![]() $e e^* = e r(e) e^* \in I$
. Thus,
$e e^* = e r(e) e^* \in I$
. Thus,
![]() $v = \sum _{e \in s^{-1}(v)} ee^* \in I$
and
$v = \sum _{e \in s^{-1}(v)} ee^* \in I$
and
![]() $v \in H_I$
. Therefore,
$v \in H_I$
. Therefore,
![]() $H_I$
is saturated. By our assumption,
$H_I$
is saturated. By our assumption,
![]() $H_I = E^0$
. This shows that I must contain all the local units of
$H_I = E^0$
. This shows that I must contain all the local units of
![]() $L_R(E)$
and thus
$L_R(E)$
and thus
![]() $I = L_R(E)$
. Hence,
$I = L_R(E)$
. Hence,
![]() $L_R(E)$
is graded simple.
$L_R(E)$
is graded simple.
Now, we show the ‘only if’ statement. Suppose that
![]() $L_R(E)$
is graded simple. Let J be a proper ideal of R. We wish to show that
$L_R(E)$
is graded simple. Let J be a proper ideal of R. We wish to show that
![]() $J = \{ 0 \}$
. To this end, let
$J = \{ 0 \}$
. To this end, let
![]() $L_J(E)$
denote the graded ideal of
$L_J(E)$
denote the graded ideal of
![]() $L_R(E)$
consisting of all elements of
$L_R(E)$
consisting of all elements of
![]() $L_R(E)$
with coefficients coming from J. Consider the natural ring homomorphism
$L_R(E)$
with coefficients coming from J. Consider the natural ring homomorphism
![]() $\varphi : L_R(E) \to L_{R/J}(E)$
. Clearly,
$\varphi : L_R(E) \to L_{R/J}(E)$
. Clearly,
![]() $\varphi $
is well defined. Note that
$\varphi $
is well defined. Note that
![]() $L_J(E) \subseteq \ker (\varphi )$
. Choose some
$L_J(E) \subseteq \ker (\varphi )$
. Choose some
![]() $u \in E^0$
. By Lemma 3.5, applied to
$u \in E^0$
. By Lemma 3.5, applied to
![]() $L_{R/J}(E)$
, it follows that
$L_{R/J}(E)$
, it follows that
![]() $u \notin \mathrm{ker}(\varphi )$
and hence
$u \notin \mathrm{ker}(\varphi )$
and hence
![]() $u \notin L_J(E)$
. Thus,
$u \notin L_J(E)$
. Thus,
![]() $L_J(E)$
is a proper graded ideal of
$L_J(E)$
is a proper graded ideal of
![]() $L_R(E)$
. By graded simplicity of
$L_R(E)$
. By graded simplicity of
![]() $L_R(E)$
, it follows that
$L_R(E)$
, it follows that
![]() $L_J(E) = \{ 0 \}$
. Thus, in particular,
$L_J(E) = \{ 0 \}$
. Thus, in particular,
![]() $Ju = \{ 0 \}$
. By Lemma 3.5 applied to
$Ju = \{ 0 \}$
. By Lemma 3.5 applied to
![]() $L_R(E)$
, we see that
$L_R(E)$
, we see that
![]() $J = \{ 0 \}$
.
$J = \{ 0 \}$
.
Let H be a proper hereditary and saturated subset of
![]() $E^0$
. Following [Reference Abrams and Aranda Pino2, Reference Abrams and Aranda Pino3], we let
$E^0$
. Following [Reference Abrams and Aranda Pino2, Reference Abrams and Aranda Pino3], we let
![]() $F:=(F^0,F^1,r,s)$
be the graph consisting of all vertices not in H and all edges whose range is not in H. For
$F:=(F^0,F^1,r,s)$
be the graph consisting of all vertices not in H and all edges whose range is not in H. For
![]() $v \in E^0$
, define
$v \in E^0$
, define
![]() $\Psi (v) := v$
if
$\Psi (v) := v$
if
![]() $v \in F^0$
, and
$v \in F^0$
, and
![]() $\Psi (v) := 0$
otherwise. For
$\Psi (v) := 0$
otherwise. For
![]() $e \in E^1$
, define
$e \in E^1$
, define
![]() $\Psi (e) := e$
if
$\Psi (e) := e$
if
![]() $e \in F^1$
, and
$e \in F^1$
, and
![]() $\Psi (e) := 0$
otherwise. Furthermore, define
$\Psi (e) := 0$
otherwise. Furthermore, define
![]() $\Psi (e^*) := e^*$
if
$\Psi (e^*) := e^*$
if
![]() $e^* \in (F^1)^*$
, and
$e^* \in (F^1)^*$
, and
![]() $\Psi (e^*) := 0$
otherwise. The argument in [Reference Abrams and Aranda Pino2, Reference Abrams and Aranda Pino3] shows that this yields a well-defined ring homomorphism
$\Psi (e^*) := 0$
otherwise. The argument in [Reference Abrams and Aranda Pino2, Reference Abrams and Aranda Pino3] shows that this yields a well-defined ring homomorphism
![]() $\Psi : L_R(E) \to L_R(F)$
. Clearly,
$\Psi : L_R(E) \to L_R(F)$
. Clearly,
![]() $\Psi $
is graded. Thus, the ideal
$\Psi $
is graded. Thus, the ideal
![]() $I := \ker (\Psi )$
of
$I := \ker (\Psi )$
of
![]() $L_R(E)$
is graded. Note that
$L_R(E)$
is graded. Note that
![]() $F^0$
is nonempty, because H is proper, and hence
$F^0$
is nonempty, because H is proper, and hence
![]() $I \neq L_R(E)$
. By our assumption,
$I \neq L_R(E)$
. By our assumption,
![]() $I=\{0\}$
. By the construction of
$I=\{0\}$
. By the construction of
![]() $\Psi $
, it follows that
$\Psi $
, it follows that
![]() $H \subseteq I$
. Thus,
$H \subseteq I$
. Thus,
![]() $H=\varnothing $
.
$H=\varnothing $
.
Definition 3.7. Define an additive map
![]() $\mathcal {L} : L_R(E) \to L_R(E)$
by requiring that
$\mathcal {L} : L_R(E) \to L_R(E)$
by requiring that
![]() $\mathcal {L}(\lambda \alpha \beta ^*) = \lambda \beta \alpha ^*$
for all
$\mathcal {L}(\lambda \alpha \beta ^*) = \lambda \beta \alpha ^*$
for all
![]() $\lambda \in R$
and
$\lambda \in R$
and
![]() $\alpha ,\beta \in E^*$
.
$\alpha ,\beta \in E^*$
.
Remark 3.8. The map
![]() $\mathcal {L}$
is an isomorphism of additive groups such that
$\mathcal {L}$
is an isomorphism of additive groups such that
![]() $\mathcal {L}((L_R(E))_N) = (L_R(E))_{-N}$
for every
$\mathcal {L}((L_R(E))_N) = (L_R(E))_{-N}$
for every
![]() $N \in \mathbb {Z}$
.
$N \in \mathbb {Z}$
.
Lemma 3.9. Suppose that
![]() $u \in E^0$
. The map
$u \in E^0$
. The map
![]() $\mathcal {L}$
restricts to an isomorphism of additive groups
$\mathcal {L}$
restricts to an isomorphism of additive groups
![]() $\mathcal {L}\lvert _{Z(u L_R(E) u)} : Z(u L_R(E) u) \to Z(u L_R(E) u)$
. In particular, the equality
$\mathcal {L}\lvert _{Z(u L_R(E) u)} : Z(u L_R(E) u) \to Z(u L_R(E) u)$
. In particular, the equality
![]() $\mathcal {L}((Z(u L_R(E) u))_N) = (Z(u L_R(E) u))_{-N}$
holds for every
$\mathcal {L}((Z(u L_R(E) u))_N) = (Z(u L_R(E) u))_{-N}$
holds for every
![]() $N \in \mathbb {Z}$
.
$N \in \mathbb {Z}$
.
Proof. Let
![]() $x = \sum _{j=1}^m \lambda _j \alpha _j \beta _j^* \in Z(u L_R(E) u)$
, where
$x = \sum _{j=1}^m \lambda _j \alpha _j \beta _j^* \in Z(u L_R(E) u)$
, where
![]() $\lambda _j \in R$
,
$\lambda _j \in R$
,
![]() $\alpha _j,\beta _j \in E^*$
and
$\alpha _j,\beta _j \in E^*$
and
![]() $s(\alpha _j)=s(\beta _j)=u$
for
$s(\alpha _j)=s(\beta _j)=u$
for
![]() $j \in \{1,\ldots ,m\}$
. Take
$j \in \{1,\ldots ,m\}$
. Take
![]() $r \in R$
. Then,
$r \in R$
. Then,
![]() $0 = xru-ru x = \sum _{j=1}^m (\lambda _j r - r \lambda _j) \alpha _j \beta _j^*$
. Therefore, we have
$0 = xru-ru x = \sum _{j=1}^m (\lambda _j r - r \lambda _j) \alpha _j \beta _j^*$
. Therefore, we have
![]() $0 = \mathcal {L}(0) = \sum _{j=1}^m (\lambda _j r - r \lambda _j) \mathcal {L}(\alpha _j \beta _j^*) = \sum _{j=1}^m ( \lambda _j r - r \lambda _j ) \beta _j \alpha _j^* = \mathcal {L}(x) ru - ru \mathcal {L}(x)$
. Thus,
$0 = \mathcal {L}(0) = \sum _{j=1}^m (\lambda _j r - r \lambda _j) \mathcal {L}(\alpha _j \beta _j^*) = \sum _{j=1}^m ( \lambda _j r - r \lambda _j ) \beta _j \alpha _j^* = \mathcal {L}(x) ru - ru \mathcal {L}(x)$
. Thus,
![]() $\mathcal {L}(x) ru = ru \mathcal {L}(x)$
. Take
$\mathcal {L}(x) ru = ru \mathcal {L}(x)$
. Take
![]() $\gamma ,\delta \in E^*$
with
$\gamma ,\delta \in E^*$
with
![]() $s(\gamma ) = s(\delta ) = u$
. Then,
$s(\gamma ) = s(\delta ) = u$
. Then,
![]() $0 = x \gamma \delta ^* - \gamma \delta ^* x = \sum _{j=1}^m \lambda _j (\alpha _j \beta _j^* \gamma \delta ^* - \gamma \delta ^* \alpha _j \beta _j^*)$
. Therefore, we have
$0 = x \gamma \delta ^* - \gamma \delta ^* x = \sum _{j=1}^m \lambda _j (\alpha _j \beta _j^* \gamma \delta ^* - \gamma \delta ^* \alpha _j \beta _j^*)$
. Therefore, we have
![]() $0 = \mathcal {L}(0) = \sum _{j=1}^m \lambda _j \mathcal {L}(\alpha _j \beta _j^* \gamma \delta ^* \kern1.4pt{-}\kern1.4pt \gamma \delta ^* \alpha _j \beta _j^*) \kern1.4pt{=}\kern1.4pt \sum _{j=1}^m \lambda _j (\delta \gamma ^* \beta _j\alpha _j^* \kern1.4pt{-}\kern1.4pt \beta _j\alpha _j^* \delta \gamma ^*) \kern1.4pt{=}\kern1.4pt \delta \gamma ^* \mathcal {L}(x) \kern1.4pt{-}\kern1.4pt \mathcal {L}(x) \delta \gamma ^*$
. Thus,
$0 = \mathcal {L}(0) = \sum _{j=1}^m \lambda _j \mathcal {L}(\alpha _j \beta _j^* \gamma \delta ^* \kern1.4pt{-}\kern1.4pt \gamma \delta ^* \alpha _j \beta _j^*) \kern1.4pt{=}\kern1.4pt \sum _{j=1}^m \lambda _j (\delta \gamma ^* \beta _j\alpha _j^* \kern1.4pt{-}\kern1.4pt \beta _j\alpha _j^* \delta \gamma ^*) \kern1.4pt{=}\kern1.4pt \delta \gamma ^* \mathcal {L}(x) \kern1.4pt{-}\kern1.4pt \mathcal {L}(x) \delta \gamma ^*$
. Thus,
![]() $\mathcal {L}(x)\delta \gamma ^* = \delta \gamma ^* \mathcal {L}(x)$
. Finally,
$\mathcal {L}(x)\delta \gamma ^* = \delta \gamma ^* \mathcal {L}(x)$
. Finally,
![]() $\mathcal {L}(x) r \delta \gamma ^* = \mathcal {L}(x) ru \delta \gamma ^* = ru \mathcal {L}(x) \delta \gamma ^* = ru \delta \gamma ^* \mathcal {L}(x) = r \delta \gamma ^* \mathcal {L}(x)$
. This shows that
$\mathcal {L}(x) r \delta \gamma ^* = \mathcal {L}(x) ru \delta \gamma ^* = ru \mathcal {L}(x) \delta \gamma ^* = ru \delta \gamma ^* \mathcal {L}(x) = r \delta \gamma ^* \mathcal {L}(x)$
. This shows that
![]() $\mathcal {L}(x) \in Z(u L_R(E) u)$
.
$\mathcal {L}(x) \in Z(u L_R(E) u)$
.
Lemma 3.10. Suppose that
![]() $u,v \in E^0$
and that
$u,v \in E^0$
and that
![]() $\alpha \in E^*$
is such that
$\alpha \in E^*$
is such that
![]() $s(\alpha ) = u$
and
$s(\alpha ) = u$
and
![]() $r(\alpha ) =~v$
. If
$r(\alpha ) =~v$
. If
![]() $x \in Z(u L_R(E) u)$
, then
$x \in Z(u L_R(E) u)$
, then
![]() $\alpha ^* x \alpha \in Z(v L_R(E) v)$
.
$\alpha ^* x \alpha \in Z(v L_R(E) v)$
.
Proof. Let
![]() $x \in Z(u L_R(E) u)$
. Take
$x \in Z(u L_R(E) u)$
. Take
![]() $y \in v L_R(E) v$
. Since
$y \in v L_R(E) v$
. Since
![]() $\alpha y \alpha ^* \in u L_R(E) u$
, it follows that
$\alpha y \alpha ^* \in u L_R(E) u$
, it follows that
![]() $y \alpha ^* x \alpha = v y \alpha ^* x \alpha = \alpha ^* \alpha y \alpha ^* x \alpha = \alpha ^* x \alpha y \alpha ^* \alpha = \alpha ^* x \alpha y v = \alpha ^* x \alpha y$
. Thus,
$y \alpha ^* x \alpha = v y \alpha ^* x \alpha = \alpha ^* \alpha y \alpha ^* x \alpha = \alpha ^* x \alpha y \alpha ^* \alpha = \alpha ^* x \alpha y v = \alpha ^* x \alpha y$
. Thus,
![]() $\alpha ^* x \alpha \in Z(v L_R(E) v)$
.
$\alpha ^* x \alpha \in Z(v L_R(E) v)$
.
Definition 3.11 [Reference Tomforde20]
Let
![]() $E=(E^0,E^1,r,s)$
be a directed graph. A cycle in E is a path
$E=(E^0,E^1,r,s)$
be a directed graph. A cycle in E is a path
![]() $\mu \in E^*\setminus E^0$
such that
$\mu \in E^*\setminus E^0$
such that
![]() $s(\mu )=r(\mu )$
. An edge
$s(\mu )=r(\mu )$
. An edge
![]() $f \in E^1$
is said to be an exit for the cycle
$f \in E^1$
is said to be an exit for the cycle
![]() $\mu =\mu _1 \ldots \mu _n$
if
$\mu =\mu _1 \ldots \mu _n$
if
![]() $s(f)=s(\mu _i)$
but
$s(f)=s(\mu _i)$
but
![]() $f \neq \mu _i$
for some
$f \neq \mu _i$
for some
![]() $i \in \{1, 2, \ldots , n\}$
.
$i \in \{1, 2, \ldots , n\}$
.
Remark 3.12. The definition of a cycle in a directed graph varies in the literature on Leavitt path algebras. In contrast to the most common definition of a cycle (see [Reference Abrams and Aranda Pino2, page 320], following [Reference Tomforde20], we allow a cycle to ‘intersect’ itself. In Theorem 1.1, the condition that ‘every cycle in E has an exit’ appears. That condition is commonly known as Condition (L). It is easy to see that Condition (L) is satisfied with the first definition of a cycle [Reference Abrams and Aranda Pino2] if and only if it is satisfied with the second definition of a cycle [Reference Tomforde20].
Remark 3.13. Let x be a nonzero element of
![]() $L_R(E)$
. It is clear from the definition of
$L_R(E)$
. It is clear from the definition of
![]() $L_R(E)$
that x can be represented as a finite sum
$L_R(E)$
that x can be represented as a finite sum
![]() $x = \sum _{i=1}^n r_i \alpha _i \beta _i^*$
, where
$x = \sum _{i=1}^n r_i \alpha _i \beta _i^*$
, where
![]() $r_i \in R \setminus \{ 0 \}$
and
$r_i \in R \setminus \{ 0 \}$
and
![]() $\alpha _i,\beta _i \in E^*$
. Following [Reference Tomforde20, Definition 4.8], we define the real degree (respectively ghost degree) of this representation as
$\alpha _i,\beta _i \in E^*$
. Following [Reference Tomforde20, Definition 4.8], we define the real degree (respectively ghost degree) of this representation as
![]() $\max \{ \deg (\alpha _i) \mid 1 \leq i \leq n \}$
(respectively
$\max \{ \deg (\alpha _i) \mid 1 \leq i \leq n \}$
(respectively
![]() $\max \{ \deg (\beta _i) \mid 1 \leq i \leq n \}$
). Note that, in general, the real degree and ghost degree of x depend on the particular choice of representation. If, however, x has a representation in only real (respectively ghost) edges, that is, if
$\max \{ \deg (\beta _i) \mid 1 \leq i \leq n \}$
). Note that, in general, the real degree and ghost degree of x depend on the particular choice of representation. If, however, x has a representation in only real (respectively ghost) edges, that is, if
![]() $x = \sum _{i=1}^n r_i \alpha _i$
(respectively
$x = \sum _{i=1}^n r_i \alpha _i$
(respectively
![]() $x = \sum _{i=1}^n r_i \beta _i^*$
), then, by Lemma 3.5, the real (respectively ghost) degree is independent of the choice of representation of x in real (respectively ghost) edges.
$x = \sum _{i=1}^n r_i \beta _i^*$
), then, by Lemma 3.5, the real (respectively ghost) degree is independent of the choice of representation of x in real (respectively ghost) edges.
Proposition 3.14. Every cycle in E has an exit if and only if for every
![]() $u \in E^0$
, the inclusion
$u \in E^0$
, the inclusion
![]() $Z(u L_R(E) u) \subseteq (u L_R(E) u)_0$
holds.
$Z(u L_R(E) u) \subseteq (u L_R(E) u)_0$
holds.
Proof. First, we show the ‘if’ statement by contrapositivity. Suppose that there is a cycle
![]() $p \in E^* \setminus E^0$
without any exit. Set
$p \in E^* \setminus E^0$
without any exit. Set
![]() $u:=s(p)$
and write
$u:=s(p)$
and write
![]() $p^0:=u$
. Take
$p^0:=u$
. Take
![]() $r \in R$
and
$r \in R$
and
![]() $\alpha ,\beta \in E^*$
with
$\alpha ,\beta \in E^*$
with
![]() $s(\alpha ) = s(\beta ) = u$
and
$s(\alpha ) = s(\beta ) = u$
and
![]() $r(\alpha )=r(\beta )$
. Since p has no exit, there are
$r(\alpha )=r(\beta )$
. Since p has no exit, there are
![]() $m,n \in \mathbb {N} \cup \{0\}$
and
$m,n \in \mathbb {N} \cup \{0\}$
and
![]() $\gamma \in E^*$
such that
$\gamma \in E^*$
such that
![]() $\alpha = p^m \gamma $
and
$\alpha = p^m \gamma $
and
![]() $\beta = p^n \gamma $
. Note that
$\beta = p^n \gamma $
. Note that
![]() $\gamma \gamma ^*=u=pp^*$
. This yields
$\gamma \gamma ^*=u=pp^*$
. This yields
![]() $p r\alpha \beta ^* = p r p^m \gamma \gamma ^* (p^*)^n = r p^{m+1} (p^*)^n$
and
$p r\alpha \beta ^* = p r p^m \gamma \gamma ^* (p^*)^n = r p^{m+1} (p^*)^n$
and
![]() $r\alpha \beta ^* p = r p^m \gamma \gamma ^* (p^*)^n p = r p^m (p^*)^n p$
. If
$r\alpha \beta ^* p = r p^m \gamma \gamma ^* (p^*)^n p = r p^m (p^*)^n p$
. If
![]() $n=0$
, then
$n=0$
, then
![]() $p^{m+1}(p^*)^n=p^{m+1}= p^m (p^*)^n p$
, and if
$p^{m+1}(p^*)^n=p^{m+1}= p^m (p^*)^n p$
, and if
![]() $n>0$
, then
$n>0$
, then
![]() $p^{m+1}(p^*)^n = p^m pp^* (p^*)^{n-1} = p^m (p^*)^{n-1} p^*p = p^m (p^*)^{n} p$
. In either case, we get
$p^{m+1}(p^*)^n = p^m pp^* (p^*)^{n-1} = p^m (p^*)^{n-1} p^*p = p^m (p^*)^{n} p$
. In either case, we get
![]() $p r\alpha \beta ^* = r\alpha \beta ^* p$
. Thus,
$p r\alpha \beta ^* = r\alpha \beta ^* p$
. Thus,
![]() $p \in Z(u L_R(E) u) \setminus (u L_R(E) u)_0$
.
$p \in Z(u L_R(E) u) \setminus (u L_R(E) u)_0$
.
Now we show the ‘only if’ statement. Suppose that every cycle in E has an exit. Take
![]() $u \in E^0$
. We wish to show that
$u \in E^0$
. We wish to show that
![]() $Z(u L_R(E) u) \subseteq (u L_R(E) u)_0$
. By Lemma 2.1(a) and Lemma 3.9, it is enough to show that
$Z(u L_R(E) u) \subseteq (u L_R(E) u)_0$
. By Lemma 2.1(a) and Lemma 3.9, it is enough to show that
![]() $(Z(u L_R(E) u))_N = \{ 0 \}$
for every negative integer N.
$(Z(u L_R(E) u))_N = \{ 0 \}$
for every negative integer N.
We now adapt parts of the proof of [Reference Abrams and Aranda Pino3, Theorem 3.1] to our situation. Take
![]() $N < 0$
. Seeking a contradiction, suppose that the set
$N < 0$
. Seeking a contradiction, suppose that the set
is nonempty. If
![]() $(u,x),(v,y) \in M$
, then we write
$(u,x),(v,y) \in M$
, then we write
![]() $(u,x) \leq (v,y)$
if x has a representation in
$(u,x) \leq (v,y)$
if x has a representation in
![]() $L_R(E)$
of real degree less than or equal to all real degrees of representations of y in
$L_R(E)$
of real degree less than or equal to all real degrees of representations of y in
![]() $L_R(E)$
. We write
$L_R(E)$
. We write
![]() $(u,x) = (v,y)$
whenever
$(u,x) = (v,y)$
whenever
![]() $(u,x) \leq (v,y)$
and
$(u,x) \leq (v,y)$
and
![]() $(v,y) \leq (u,x)$
. Clearly,
$(v,y) \leq (u,x)$
. Clearly,
![]() $\leq $
is a total order on M which therefore has a minimal element
$\leq $
is a total order on M which therefore has a minimal element
![]() $(u,x)$
. Choose a minimising representation
$(u,x)$
. Choose a minimising representation
![]() $x = \sum _{i=1}^n e_i a_i + b$
, where
$x = \sum _{i=1}^n e_i a_i + b$
, where
![]() $e_1,\ldots ,e_n \in E^1$
are all distinct, each
$e_1,\ldots ,e_n \in E^1$
are all distinct, each
![]() $a_i \in L_R(E)$
is either zero or nonzero and representable as an element of smaller real degree than that of x, and b is a polynomial (possibly zero) in only ghost paths whose source and range equals u. Take
$a_i \in L_R(E)$
is either zero or nonzero and representable as an element of smaller real degree than that of x, and b is a polynomial (possibly zero) in only ghost paths whose source and range equals u. Take
![]() $i\in \{1,\ldots ,n\}$
. Write
$i\in \{1,\ldots ,n\}$
. Write
![]() $v_i := r(e_i)$
. By Lemma 3.10,
$v_i := r(e_i)$
. By Lemma 3.10,
![]() $e_i^* x e_i \in (Z(v_i L_R(E) v_i))_N$
. Since
$e_i^* x e_i \in (Z(v_i L_R(E) v_i))_N$
. Since
![]() $e_i^* x e_i$
is of smaller real degree than x, it follows that
$e_i^* x e_i$
is of smaller real degree than x, it follows that
![]() $e_i^* x e_i = 0$
. Further, since
$e_i^* x e_i = 0$
. Further, since
![]() $x \in (Z(u L_R(E) u))_N$
, it follows that
$x \in (Z(u L_R(E) u))_N$
, it follows that
![]() $e_i^* x = e_i^* e_i e_i^* x = e_i^* x e_i e_i^* = 0$
. Thus,
$e_i^* x = e_i^* e_i e_i^* x = e_i^* x e_i e_i^* = 0$
. Thus,
![]() $0 = e_i^* x = a_i + e_i^* b$
and hence
$0 = e_i^* x = a_i + e_i^* b$
and hence
![]() $a_i = -e_i^* b$
.
$a_i = -e_i^* b$
.
Now,
![]() $0 \neq x = (u - \sum _{i=1}^n e_i e_i^*)b$
. Thus,
$0 \neq x = (u - \sum _{i=1}^n e_i e_i^*)b$
. Thus,
![]() $u \neq \sum _{i=1}^n e_i e_i^*$
and
$u \neq \sum _{i=1}^n e_i e_i^*$
and
![]() $b\neq 0$
. This implies that there is some
$b\neq 0$
. This implies that there is some
![]() $f \in E^1 \setminus \{e_1,\ldots ,e_n\}$
with
$f \in E^1 \setminus \{e_1,\ldots ,e_n\}$
with
![]() $s(f) = u$
. Furthermore,
$s(f) = u$
. Furthermore,
![]() $f^* x = f^* b$
, and, by Lemma 3.5,
$f^* x = f^* b$
, and, by Lemma 3.5,
![]() $f^* b \neq 0$
since it is a sum of distinct ghost paths. Write
$f^* b \neq 0$
since it is a sum of distinct ghost paths. Write
![]() $v:=r(f)$
. By Lemma 3.10, it follows that
$v:=r(f)$
. By Lemma 3.10, it follows that
![]() $f^* x f \in (Z(v L_R(E) v))_N$
. Observing that
$f^* x f \in (Z(v L_R(E) v))_N$
. Observing that
![]() $0 \neq f^* x = f^* f f^* x = f^* x f f^*$
, we get
$0 \neq f^* x = f^* f f^* x = f^* x f f^*$
, we get
![]() $f^* x f \neq 0$
. Note that the real degree of
$f^* x f \neq 0$
. Note that the real degree of
![]() $f^* x f$
is less than or equal to the real degree of x. Hence, by the assumption made on
$f^* x f$
is less than or equal to the real degree of x. Hence, by the assumption made on
![]() $(u,x)$
, and possibly after replacing
$(u,x)$
, and possibly after replacing
![]() $(u,x)$
by
$(u,x)$
by
![]() $(v,f^*xf)$
, we may assume that
$(v,f^*xf)$
, we may assume that
![]() $a_i=0$
for every
$a_i=0$
for every
![]() $i\in \{1,\ldots ,n\}$
. Therefore, suppose that
$i\in \{1,\ldots ,n\}$
. Therefore, suppose that
![]() $x = \sum _{j=1}^m r_j \beta _j^*$
for some nonzero
$x = \sum _{j=1}^m r_j \beta _j^*$
for some nonzero
![]() $r_j \in R$
and some distinct paths
$r_j \in R$
and some distinct paths
![]() $\beta _j \in E^{-N}$
with
$\beta _j \in E^{-N}$
with
![]() $s(\beta _j)=r(\beta _j) = u$
. Take
$s(\beta _j)=r(\beta _j) = u$
. Take
![]() $k \in \{ 1,\ldots ,m \}$
. By Lemma 3.10, it follows that
$k \in \{ 1,\ldots ,m \}$
. By Lemma 3.10, it follows that
![]() $r_k \beta _k^* = \beta _k^* x \beta _k \in Z(u L_R(E) u)$
. By assumption, the cycle
$r_k \beta _k^* = \beta _k^* x \beta _k \in Z(u L_R(E) u)$
. By assumption, the cycle
![]() $\beta _k$
has an exit at some
$\beta _k$
has an exit at some
![]() $w \in E^0$
. Thus, there are
$w \in E^0$
. Thus, there are
![]() $\gamma ,\delta \in E^*$
and
$\gamma ,\delta \in E^*$
and
![]() $\epsilon \in E^1$
such that
$\epsilon \in E^1$
such that
![]() $\beta _k = \gamma \delta $
,
$\beta _k = \gamma \delta $
,
![]() $r(\gamma ) = s(\epsilon )=w$
and
$r(\gamma ) = s(\epsilon )=w$
and
![]() $\epsilon ^* \delta = 0$
. By Lemma 3.10, it follows that
$\epsilon ^* \delta = 0$
. By Lemma 3.10, it follows that
![]() $r_k (\delta \gamma )^* = r_k \gamma ^* \delta ^* \gamma ^*\gamma = \gamma ^* r_k \beta _k^* \gamma \in Z(w L_R(E) w)$
. We now reach a contradiction, because
$r_k (\delta \gamma )^* = r_k \gamma ^* \delta ^* \gamma ^*\gamma = \gamma ^* r_k \beta _k^* \gamma \in Z(w L_R(E) w)$
. We now reach a contradiction, because
![]() $0 \neq \epsilon \epsilon ^* r_k (\delta \gamma )^* = r_k (\delta \gamma )^* \epsilon \epsilon ^* = 0$
.
$0 \neq \epsilon \epsilon ^* r_k (\delta \gamma )^* = r_k (\delta \gamma )^* \epsilon \epsilon ^* = 0$
.
Now, we prove our main result.
Proof of Theorem 1.1
First, we show the ‘only if’ statement. Suppose that
![]() $L_R(E)$
is simple. Then
$L_R(E)$
is simple. Then
![]() $L_R(E)$
is graded simple and hence, by Proposition 3.6, it follows that R is simple and that
$L_R(E)$
is graded simple and hence, by Proposition 3.6, it follows that R is simple and that
![]() $E^0$
has no nontrivial hereditary and saturated subset. Furthermore, Proposition 2.4 implies that
$E^0$
has no nontrivial hereditary and saturated subset. Furthermore, Proposition 2.4 implies that
![]() $uL_R(E)u$
is simple for every
$uL_R(E)u$
is simple for every
![]() $u \in E^0$
, and hence, by Proposition 2.2,
$u \in E^0$
, and hence, by Proposition 2.2,
![]() $Z(uL_R(E)u) \subseteq (uL_R(E)u)_0$
for every
$Z(uL_R(E)u) \subseteq (uL_R(E)u)_0$
for every
![]() $u \in E^0$
. Thus, by Proposition 3.14, every cycle in E has an exit.
$u \in E^0$
. Thus, by Proposition 3.14, every cycle in E has an exit.
Now we show the ‘if’ statement. Suppose that R is simple,
![]() $E^0$
has no nontrivial hereditary and saturated subset, and every cycle in E has an exit. By Proposition 3.6,
$E^0$
has no nontrivial hereditary and saturated subset, and every cycle in E has an exit. By Proposition 3.6,
![]() $L_R(E)$
is graded simple. Take
$L_R(E)$
is graded simple. Take
![]() $u \in E^0$
. It follows from Proposition 3.14 that
$u \in E^0$
. It follows from Proposition 3.14 that
![]() $Z(uL_R(E)u) \subseteq (uL_R(E)u)_0$
. Furthermore, by Proposition 2.4,
$Z(uL_R(E)u) \subseteq (uL_R(E)u)_0$
. Furthermore, by Proposition 2.4,
![]() $uL_R(E)u$
is graded simple. Thus, by Proposition 2.2,
$uL_R(E)u$
is graded simple. Thus, by Proposition 2.2,
![]() $uL_R(E)u$
is simple. Hence, by Proposition 2.5,
$uL_R(E)u$
is simple. Hence, by Proposition 2.5,
![]() $L_R(E)$
is simple.
$L_R(E)$
is simple.
4 The centre of a simple Leavitt path algebra
In this section, we prove Theorem 1.2 using results from the previous sections together with some auxiliary observations.
Remark 4.1. Let
![]() $E=(E^0,E^1,r,s)$
be a directed graph.
$E=(E^0,E^1,r,s)$
be a directed graph.
(a) Take
![]() $v \in E^0$
. We write
$v \in E^0$
. We write
![]() $w \leq v$
, for
$w \leq v$
, for
![]() $w \in E^0$
, if there is
$w \in E^0$
, if there is
![]() $\mu \in E^*$
with
$\mu \in E^*$
with
![]() $s(\mu )=v$
and
$s(\mu )=v$
and
![]() $r(\mu )=w$
. The set
$r(\mu )=w$
. The set
![]() $T(v) := \{ w \in E^0 \mid w \leq v \}$
is the smallest hereditary subset of
$T(v) := \{ w \in E^0 \mid w \leq v \}$
is the smallest hereditary subset of
![]() $E^0$
containing v.
$E^0$
containing v.
(b) Suppose that
![]() $X \subseteq E^0$
. Put
$X \subseteq E^0$
. Put
![]() $T(X) := \bigcup _{x \in X} T(x)$
. The hereditary saturated closure
$T(X) := \bigcup _{x \in X} T(x)$
. The hereditary saturated closure
![]() $\overline {X}$
of X is defined as the smallest hereditary and saturated subset of
$\overline {X}$
of X is defined as the smallest hereditary and saturated subset of
![]() $E^0$
containing X. One can show (see [Reference Aranda Pino and Crow6, page 626] and the references therein) that
$E^0$
containing X. One can show (see [Reference Aranda Pino and Crow6, page 626] and the references therein) that
![]() $\overline {X} = \bigcup _{n=0}^{\infty } X_n$
, where
$\overline {X} = \bigcup _{n=0}^{\infty } X_n$
, where
![]() $X_0 := T(X)$
and
$X_0 := T(X)$
and
![]() $X_n := \{ y \in E^0 \mid 0 < |s^{-1}(y)| < \infty \ \mbox {and} \ r( s^{-1}(y) ) \subseteq X_{n-1} \} \cup X_{n-1}$
for
$X_n := \{ y \in E^0 \mid 0 < |s^{-1}(y)| < \infty \ \mbox {and} \ r( s^{-1}(y) ) \subseteq X_{n-1} \} \cup X_{n-1}$
for
![]() $n \geq 1$
.
$n \geq 1$
.
The following result can be proved by induction (see [Reference Lännström, Lundström, Öinert and Wagner14, Proposition 14.11] and [Reference Tomforde20, Lemma 5.2]).
Proposition 4.2. Suppose that R is an associative unital ring and that
![]() $E=(E^0,E^1,r,s)$
is a directed graph. If
$E=(E^0,E^1,r,s)$
is a directed graph. If
![]() $a \in (L_R(E))_0$
is nonzero, then there exist
$a \in (L_R(E))_0$
is nonzero, then there exist
![]() $\alpha , \beta \in E^*$
,
$\alpha , \beta \in E^*$
,
![]() $v \in E^0$
and a nonzero
$v \in E^0$
and a nonzero
![]() $k \in R$
such that
$k \in R$
such that
![]() $\alpha ^* a \beta = kv$
.
$\alpha ^* a \beta = kv$
.
Now, we prove our second main result.
Proof of Theorem 1.2
Write
![]() $S := L_R(E)$
. If S is not unital, then it follows immediately from [Reference Wisbauer21, Ch. 1, Section 3.3] that
$S := L_R(E)$
. If S is not unital, then it follows immediately from [Reference Wisbauer21, Ch. 1, Section 3.3] that
![]() $Z(S)=\{0\}$
. This proves item (a). Now, we show item (b). Suppose that S is unital, that is,
$Z(S)=\{0\}$
. This proves item (a). Now, we show item (b). Suppose that S is unital, that is,
![]() $E^0$
is finite. Take a nonzero
$E^0$
is finite. Take a nonzero
![]() $x \in Z(S)$
. By Proposition 2.2, it follows that
$x \in Z(S)$
. By Proposition 2.2, it follows that
![]() $x \in S_0$
. Therefore, by Proposition 4.2, there are
$x \in S_0$
. Therefore, by Proposition 4.2, there are
![]() $\alpha ,\beta \in E^*$
,
$\alpha ,\beta \in E^*$
,
![]() $v \in E^0$
and a nonzero
$v \in E^0$
and a nonzero
![]() $k \in R$
such that
$k \in R$
such that
![]() $\alpha ^* x \beta = kv$
. From this equality, the grading and the fact that
$\alpha ^* x \beta = kv$
. From this equality, the grading and the fact that
![]() $x \in Z(S)$
, it follows that
$x \in Z(S)$
, it follows that
![]() $\alpha =\beta $
and
$\alpha =\beta $
and
![]() $r(\alpha )=v$
. Hence,
$r(\alpha )=v$
. Hence,
![]() $vx = \alpha ^*\alpha x = \alpha ^* x\alpha = \alpha ^* x \beta = kv$
. The equality
$vx = \alpha ^*\alpha x = \alpha ^* x\alpha = \alpha ^* x \beta = kv$
. The equality
![]() $vx = kv$
implies that
$vx = kv$
implies that
![]() $k \in Z(R)$
. Put
$k \in Z(R)$
. Put
![]() $X := \{ v \}$
. Then,
$X := \{ v \}$
. Then,
![]() $\overline {X}$
is a nonempty hereditary and saturated subset of
$\overline {X}$
is a nonempty hereditary and saturated subset of
![]() $E^0$
. By Theorem 1.1,
$E^0$
. By Theorem 1.1,
![]() $\overline {X} = E^0$
. We claim that this implies that
$\overline {X} = E^0$
. We claim that this implies that
![]() $wx = kw$
for every
$wx = kw$
for every
![]() $w \in E^0$
. Let us assume, for a moment, that this claim holds. Then,
$w \in E^0$
. Let us assume, for a moment, that this claim holds. Then,
![]() $x = 1_S \cdot x = \sum _{w \in E^0} wx = \sum _{w \in E^0} kw = k \cdot \sum _{w \in E^0} w = k \cdot 1_S \in Z(R) \cdot 1_S$
. Thus,
$x = 1_S \cdot x = \sum _{w \in E^0} wx = \sum _{w \in E^0} kw = k \cdot \sum _{w \in E^0} w = k \cdot 1_S \in Z(R) \cdot 1_S$
. Thus,
![]() $Z(S) \subseteq Z(R) \cdot 1_S$
. Clearly,
$Z(S) \subseteq Z(R) \cdot 1_S$
. Clearly,
![]() $Z(R) \cdot 1_S \subseteq Z(S)$
holds.
$Z(R) \cdot 1_S \subseteq Z(S)$
holds.
Now we show the claim. We will use induction to prove that for every
![]() $n \geq 0$
, the implication
$n \geq 0$
, the implication
![]() $w \in X_n \Rightarrow wx = kw$
holds. From this, the claim follows. Base case:
$w \in X_n \Rightarrow wx = kw$
holds. From this, the claim follows. Base case:
![]() $n=0$
. Suppose that
$n=0$
. Suppose that
![]() $w\in X_0$
, that is,
$w\in X_0$
, that is,
![]() $w \leq v$
. Then, there is a path
$w \leq v$
. Then, there is a path
![]() $\delta $
from v to w. This gives
$\delta $
from v to w. This gives
![]() $wx = \delta ^* \delta x = \delta ^* v \delta x = \delta ^* vx \delta = \delta ^* kv \delta = k \delta ^* v \delta = k \delta ^* \delta = k w$
. Induction step: Suppose that
$wx = \delta ^* \delta x = \delta ^* v \delta x = \delta ^* vx \delta = \delta ^* kv \delta = k \delta ^* v \delta = k \delta ^* \delta = k w$
. Induction step: Suppose that
![]() $wx = kw$
for every
$wx = kw$
for every
![]() $w \in X_{n-1}$
. Take
$w \in X_{n-1}$
. Take
![]() $y \in X_n \setminus X_{n-1}$
and note that
$y \in X_n \setminus X_{n-1}$
and note that
![]() $0 < |s^{-1}(y)| < \infty $
and
$0 < |s^{-1}(y)| < \infty $
and
![]() $r( s^{-1}(y) ) \subseteq X_{n-1}$
. Then,
$r( s^{-1}(y) ) \subseteq X_{n-1}$
. Then,
![]() $yx = \sum _{e \in s^{-1}(y)} e e^* x = \sum _{e \in s^{-1}(y)} e r(e) x e^* = \sum _{e \in s^{-1}(y)} e k r(e) e^* = k \sum _{e \in s^{-1}(y)} e e^* = ky$
.
$yx = \sum _{e \in s^{-1}(y)} e e^* x = \sum _{e \in s^{-1}(y)} e r(e) x e^* = \sum _{e \in s^{-1}(y)} e k r(e) e^* = k \sum _{e \in s^{-1}(y)} e e^* = ky$
.