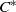Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Perera, Francesc
Toms, Andrew
White, Stuart
and
Winter, Wilhelm
2014.
The Cuntz semigroup and stability of closeC∗-algebras.
Analysis & PDE,
Vol. 7,
Issue. 4,
p.
929.
Qian, Wenhua
and
Shen, Junhao
2016.
Similarity Degree of a Class of C $${^*}$$ ∗ -Algebras.
Integral Equations and Operator Theory,
Vol. 84,
Issue. 1,
p.
121.
Pop, Florin
2017.
Similarities of Tensor Products of Type $$\mathrm {II}_1$$ II 1 Factors.
Integral Equations and Operator Theory,
Vol. 89,
Issue. 3,
p.
455.
HADWIN, DON
LI, WEIHUA
LIU, WENJING
and
SHEN, JUNHAO
2019.
A CHARACTERISATION OF TRACIALLY NUCLEAR C*-ALGEBRAS.
Bulletin of the Australian Mathematical Society,
Vol. 100,
Issue. 1,
p.
119.
Hadwin, Don
and
Shen, Junhao
2022.
A modified similarity degree for C*-algebras.
Acta Scientiarum Mathematicarum,
Vol. 88,
Issue. 3-4,
p.
627.