Published online by Cambridge University Press: 17 April 2009
Recently, Varshney and Singh [Rend. Mat. (6) 2 (1982), 219–225] have given sharper quantitative estimates of convergence for Bernstein polynomials, Szasz and Meyer-Konig-Zeller operators. We have achieved improvement over these estimates by taking moments of higher order. For example, in case of the Meyer-Konig-Zeller operator, they gave the following estimate
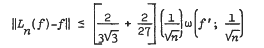
wherein ∥·∥ stands for sup norm. We have improved this result to
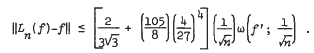
We may remark here that for this modulus of continuity 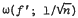 ) our result cannot be sharpened further by taking higher order moments.
) our result cannot be sharpened further by taking higher order moments.