Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-31T14:35:41.418Z Has data issue: false hasContentIssue false
  • English
  • Français

SHAPIRO’S UNCERTAINTY PRINCIPLE IN THE DUNKL SETTING

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  29 April 2015

SAIFALLAH GHOBBER
SAIFALLAH GHOBBER*
Affiliation:
Université de Tunis El Manar, Faculté des Sciences de Tunis, LR11ES11 Analyse Mathématiques et Applications, 2092, Tunis, Tunisie email [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

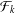The Dunkl transform ${\mathcal{F}}_{k}$ is a generalisation of the usual Fourier transform to an integral transform invariant under a finite reflection group. The goal of this paper is to prove a strong uncertainty principle for orthonormal bases in the Dunkl setting which states that the product of generalised dispersions cannot be bounded for an orthonormal basis. Moreover, we obtain a quantitative version of Shapiro’s uncertainty principle on the time–frequency concentration of orthonormal sequences and show, in particular, that if the elements of an orthonormal sequence and their Dunkl transforms have uniformly bounded dispersions then the sequence is finite.

Keywords

Dunkl transformShapiro’s uncertainty principlephase space localisationtime–frequency concentration

MSC classification

Secondary: 42C20: Other transformations of harmonic type
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 1 , August 2015 , pp. 98 - 110
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Benedetto, J. J., ‘On frame decompositions, sampling and uncertainty principle inequalities’, in: Wavelets: Mathematics and Applications, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1994), 247–304.Google Scholar
Bourgain, J., ‘A remark on the uncertainty principle for Hilbertian basis’, J. Funct. Anal. 79 (1998), 136–143.CrossRefGoogle Scholar
de Bruijn, N. G, ‘Uncertainty principles in Fourier analysis’, in: Inequalities (Proc. Symp. Wright–Patterson Air Force Base, OH, 1965) (Academic Press, New York, 1967), 57–71.Google Scholar
de Jeu, M. F. E., ‘The Dunkl transform’, Invent. Math. 113 (1993), 147–162.CrossRefGoogle Scholar
Dunkl, C. F., ‘Differential-difference operators associated to reflection groups’, Trans. Amer. Math. Soc. 311 (1989), 167–183.CrossRefGoogle Scholar
Dunkl, C. F., ‘Integral kernels with reflection group invariance’, Canad. J. Math. 43 (1991), 1213–1227.CrossRefGoogle Scholar
Dunkl, C. F., ‘Hankel transforms associated to finite reflection groups’, in: Hypergeometric Functions on Domains of Positivity, Jack Polynomials, and Applications (Tampa, FL, 1991), Contemp. Math., 138 (American Mathematical Society, Providence, RI, 1992), 123–138.CrossRefGoogle Scholar
Ghobber, S., ‘Phase space localization of orthonormal sequences in L 𝛼2(ℝ+)’, J. Approx. Theory. 189 (2015), 123–136.CrossRefGoogle Scholar
Ghobber, S. and Jaming, Ph., ‘Uncertainty principles for integral operators’, Studia Math. 220 (2014), 197–220.CrossRefGoogle Scholar
Gohberg, I., Goldberg, S. and Krupnik, N., ‘Traces and determinants of linear operators’, in: Operator Theory: Advances and Applications, 116 (Birkhäuser, Basel, 2000).Google Scholar
Gröchenig, K. and Malinnikova, E., ‘Phase space localization of Riesz bases for L 2(ℝd)’, Rev. Mat. Iberoam. 29 (2013), 115–134.CrossRefGoogle Scholar
Jaming, Ph. and Powell, A. M., ‘Uncertainty principles for orthonormal sequences’, J. Funct. Anal. 243 (2007), 611–630.CrossRefGoogle Scholar
Lapointe, L. and Vinet, L., ‘Exact operator solution of the Calogero–Sutherland model’, Comm. Math. Phys. 178 (1996), 425–452.CrossRefGoogle Scholar
Malinnikova, E., ‘Orthonormal sequences in L 2(ℝd) and time frequency localization’, J. Fourier Anal. Appl. 16 (2010), 983–1006.CrossRefGoogle Scholar
Polychronakos, A. P., ‘Exchange operator formalism for integrable systems of particles’, Phys. Rev. Lett. 69 (1992), 703–705.CrossRefGoogle ScholarPubMed
Powell, A. M., ‘Time–frequency mean and variance sequences of orthonormal bases’, J. Fourier Anal. Appl. 11 (2005), 375–387.CrossRefGoogle Scholar
Rösler, M., ‘An uncertainty principle for the Dunkl transform’, Bull. Aust. Math. Soc. 59 (1999), 353–360.CrossRefGoogle Scholar
Rösler, M., ‘Generalized Hermite polynomials and the heat equation for the Dunkl operators’, Comm. Math. Phys. 192 (1998), 519–542.Google Scholar
Rösler, M. and Voit, M., ‘Markov processes with Dunkl operators’, Adv. Appl. Math. 21 (1998), 575–643.CrossRefGoogle Scholar
Shapiro, H. S., Uncertainty principles for basis in $L^{2}(\mathbb{R})$, 1991. Unpublished manuscript.Google Scholar
Shimeno, N., ‘A note on the uncertainty principle for the Dunkl transform’, J. Math. Sci. Univ. Tokyo 8 (2001), 33–42.Google Scholar
Soltani, S., ‘Heisenberg–Pauli–Weyl uncertainty inequality for the Dunkl transform on ℝd’, Bull. Aust. Math. Soc. 87 (2013), 316–325.CrossRefGoogle Scholar