Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-08T16:06:38.435Z Has data issue: false hasContentIssue false
  • English
  • Français

SETS WITH ALMOST COINCIDING REPRESENTATION FUNCTIONS

Part of: Sequences and sets

Published online by Cambridge University Press:  28 June 2013

SÁNDOR Z. KISS ,
ESZTER ROZGONYI  and
CSABA SÁNDOR
SÁNDOR Z. KISS*
Affiliation:
Institute of Mathematics, Budapest University of Technology and Economics, H-1529 Budapest, PO Box 91, Hungary email [email protected]@math.bme.hu Computer and Automation Research Institute of the Hungarian Academy of Sciences, Lágymányosi utca 11, H-1111 Budapest, Hungary
ESZTER ROZGONYI
Affiliation:
Institute of Mathematics, Budapest University of Technology and Economics, H-1529 Budapest, PO Box 91, Hungary email [email protected]@math.bme.hu
CSABA SÁNDOR
Affiliation:
Institute of Mathematics, Budapest University of Technology and Economics, H-1529 Budapest, PO Box 91, Hungary email [email protected]@math.bme.hu
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a given integer $n$ and a set 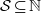$ \mathcal{S} \subseteq \mathbb{N} $, denote by 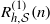${ R}_{h, \mathcal{S} }^{(1)} (n)$ the number of solutions of the equation 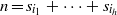$n= {s}_{{i}_{1} } + \cdots + {s}_{{i}_{h} } $, 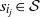${s}_{{i}_{j} } \in \mathcal{S} $, 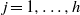$j= 1, \ldots , h$. In this paper we determine all pairs 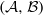$( \mathcal{A} , \mathcal{B} )$, 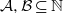$ \mathcal{A} , \mathcal{B} \subseteq \mathbb{N} $, for which 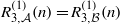${ R}_{3, \mathcal{A} }^{(1)} (n)= { R}_{3, \mathcal{B} }^{(1)} (n)$ from a certain point on. We discuss some related problems.

Keywords

additive number theoryrepresentation functions

MSC classification

Secondary: 11B34: Representation functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 97 - 111
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Chen, Y.-G. and Tang, M., ‘Partitions of natural numbers with the same representation functions’, J. Number Theory 129 (2009), 2689–2695.Google Scholar
Chen, Y.-G. and Wang, B., ‘On additive properties of two special sequences’, Acta Arith. 110.3 (2003), 299–303.Google Scholar
Dombi, G., ‘Additive properties of certain sets’, Acta Arith. 103.2 (2002), 137–146.Google Scholar
Kronecker, L., ‘Zwei Sätze über Gleichungen mit ganzzahligen Coefficienten’, J. reine angew. Math. 53 (1857), 173–175.Google Scholar
Lev, V. F., ‘Reconstructing integer sets from their representation functions’, Electr. J. Combin. 11 (2004), R78.CrossRefGoogle Scholar
Nathanson, M. B., ‘Representation functions of sequences in additive number theory’, Proc. Amer. Math. Soc. 72 (1978), 16–20.CrossRefGoogle Scholar
Sándor, Cs., ‘Partitions of natural numbers and their representation functions’, Integers 4 (2004), A18.Google Scholar
Tang, M., ‘Partitions of the set of natural numbers and their representation functions’, Discrete Math. 308 (2008), 2614–2616.Google Scholar
Yang, Q.-H., ‘Another proof of Nathanson’s theorems’, J. Integer Sequences 14 (2011).Google Scholar