Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T05:07:35.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Set covering number for a finite set

Published online by Cambridge University Press:  17 April 2009

H.-C. Chang  and
N. Prabhu
H.-C. Chang
Affiliation:
Department of MathematicsPurdue University MGL 1303West Lafayette IN 47907United States of America
N. Prabhu
Affiliation:
Department of MathematicsPurdue University MGL 1303West Lafayette IN 47907United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a finite set S of cardinality N, the minimum number of j-subsets of S needed to cover all the r-subsets of S is called the covering number C(N, j, r). While Erdös and Hanani's conjecture that 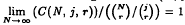was proved by Rödl, no nontrivial upper bound for C(N, j, r) was known for finite N. In this note we obtain a nontrivial upper bound by showing that for finite N,

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 53 , Issue 2 , April 1996 , pp. 267 - 269
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Erdös, P. and Hanani, H., ‘On a limit theorem in combinatorial analysis’, publ. Math. Debrecen 10 (1963), 10–13.CrossRefGoogle Scholar
[2]Rö, V., ‘On a packing and coverkng problem’, European J. Combin. 5 (1985), 69–78.Google Scholar