No CrossRef data available.
Article contents
THE ROBIN PROBLEM FOR THE HÉNON EQUATION
Part of:
Elliptic equations and systems
Published online by Cambridge University Press: 27 June 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, we consider the following Robin problem: 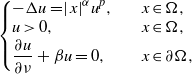where 
$$\begin{eqnarray*}\displaystyle \left\{ \begin{array}{ @{}ll@{}} \displaystyle - \Delta u= \mid x{\mathop{\mid }\nolimits }^{\alpha } {u}^{p} , \quad & \displaystyle x\in \Omega , \\ \displaystyle u\gt 0, \quad & \displaystyle x\in \Omega , \\ \displaystyle \displaystyle \frac{\partial u}{\partial \nu } + \beta u= 0, \quad & \displaystyle x\in \partial \Omega , \end{array} \right.&&\displaystyle\end{eqnarray*}$$
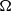$\Omega $ is the unit ball in 
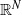${ \mathbb{R} }^{N} $ centred at the origin, with 
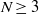$N\geq 3$, 
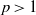$p\gt 1$, 
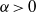$\alpha \gt 0$, 
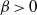$\beta \gt 0$, and 
$\nu $ is the unit outward vector normal to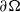 
$\partial \Omega $. We prove that the above problem has no solution when 
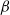$\beta $ is small enough. We also obtain existence results and we analyse the symmetry breaking of the ground state solutions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Auchmuty, G., ‘Steklov eigenproblems and the representation of solutions of elliptic boundary value problems’, Numer. Funct. Anal. Optim. 25 (3–4) (2004), 321–348.CrossRefGoogle Scholar
Badiale, M. and Serra, E., ‘Multiplicity results for the supercritical Hénon equation’, Adv. Nonlinear Stud. 4 (2004), 453–467.CrossRefGoogle Scholar
Bandle, C., Isoperimetric Inequalities and Applications, Monographs and Studies in Mathematics, 7 (Pitman, Boston, 1980).Google Scholar
Byeon, J. and Wang, Z.-Q., ‘On the Hénon equation: asymptotic profile of ground state I’, Ann. Inst. H. Poincaré Anal. Non Linéaire 23 (2006), 803–828.CrossRefGoogle Scholar
Byeon, J. and Wang, Z.-Q., ‘On the Hénon equation: asymptotic profile of ground state II’, J. Differential Equations 216 (2005), 78–108.CrossRefGoogle Scholar
Cao, D. and Peng, S., ‘The asymptotic behavior of the ground state solutions for Hénon equation’, J. Math. Anal. Appl. 278 (2003), 1–17.CrossRefGoogle Scholar
Chen, G., Ni, W. M. and Zhou, J., ‘Algorithms and visualization for solutions of nonlinear elliptic equations’, Internat. J. Bifur. Chaos Appl. Sci. Engrg. 10 (2000), 1565–1612.CrossRefGoogle Scholar
Gazzini, M. and Serra, E., ‘The Neumann problem for the Hénon equation, trace inequalities and Steklov eigenvalues’, Ann. Inst. H. Poincaré Anal. Non Linéaire 25 (2008), 281–302.CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L., ‘Symmetry of positive solutions of nonlinear elliptic equations in 
${ \mathbb{R} }^{N} $’, in: Mathematical Analysis and Applications, Part A, Advances in Mathematics, Supplementary Studies, 7 (Academic Press, New York, 1981), 369–402.Google Scholar
${ \mathbb{R} }^{N} $’, in: Mathematical Analysis and Applications, Part A, Advances in Mathematics, Supplementary Studies, 7 (Academic Press, New York, 1981), 369–402.Google ScholarGidas, B. and Spruck, J., ‘A priori bounds for positive solutions of nonlinear elliptic equations’, Comm. Partial Differential Equations 8 (1981), 883–901.CrossRefGoogle Scholar
Gidas, B. and Spruck, J., ‘Global and local behavior of positive solutions of nonlinear elliptic equations’, Comm. Pure Appl. Math. 34 (1981), 525–598.CrossRefGoogle Scholar
Hénon, M., ‘Numerical experiments on the stability of spherical stellar systems’, Astronom. Astrophys. Lib. 24 (1973), 229–238.Google Scholar
Morrey, C. B., Multiple Integrals in the Calculus of Variations (Springer, New York, 1966).CrossRefGoogle Scholar
Ni, W. M., ‘A nonlinear Dirichlet problem on the unit ball and its applications’, Indiana Univ. Math. J. 31 (1982), 801–807.CrossRefGoogle Scholar
Pistoia, A. and Serra, E., ‘Multi-peak solutions for the Hénon equation with slightly subcritical growth’, Math. Z. 256 (2007), 75–97.CrossRefGoogle Scholar
Serra, E., ‘Nonradial positive solutions for the Hénon equation with critical growth’, Calc. Var. Partial Differential Equations 23 (2005), 301–326.CrossRefGoogle Scholar
Smets, D., Su, J. B. and Willem, M., ‘Nonradial ground states for the Hénon equation’, Commun. Contemp. Math. 4 (2002), 467–480.CrossRefGoogle Scholar
Smets, D. and Willem, M., ‘Partial symmetry and asymptotic behavior for some elliptic variational problems’, Calc. Var. Partial Differential Equations 18 (2003), 57–75.CrossRefGoogle Scholar
You have
Access