No CrossRef data available.
Published online by Cambridge University Press: 13 October 2022
Suppose M is a complex projective manifold of dimension 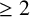 $\geq 2$, V is the support of an ample divisor in M and U is an open set in M that intersects each irreducible component of V. We show that a pluriharmonic map
$\geq 2$, V is the support of an ample divisor in M and U is an open set in M that intersects each irreducible component of V. We show that a pluriharmonic map 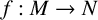 $f:M\to N$ into a Kähler manifold N is holomorphic whenever
$f:M\to N$ into a Kähler manifold N is holomorphic whenever  $f\vert _{V\,\cap \, U}$ is holomorphic.
$f\vert _{V\,\cap \, U}$ is holomorphic.