Published online by Cambridge University Press: 17 April 2009
Sargent and later Bullen and Mukhopadhyay obtained a definition of absolutely continuous functions, 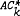 functions, that is related to kth Peano derivatives. The generalised notions of ACkG*, [ACkG*], ACkG* above, etcetera functions led Bullen and Mukhopadhyay to define certain general integrals of the kth order.
functions, that is related to kth Peano derivatives. The generalised notions of ACkG*, [ACkG*], ACkG* above, etcetera functions led Bullen and Mukhopadhyay to define certain general integrals of the kth order.
The present work is concerned with a further simplification of the definitions of such functions by the use of divided differences but still retaining similar fundamental properties. These concepts lead to the introduction of Denjoy and Ridder type integrals which are shown to be equivalent to a Perron type integral that corresponds to kth Riemann* derivatives. All three of these integrals are shown to be equivalent to the three integrals of Bullen and Mukhopadhyay.