Let 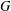$G$ be a finite abelian group, 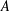$A$ a nonempty subset of 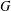$G$ and 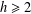$h\geq 2$ an integer. For 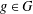$g\in G$, let 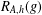$R_{A,h}(g)$ denote the number of solutions of the equation 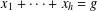$x_{1}+\cdots +x_{h}=g$ with 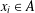$x_{i}\in A$ for 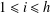$1\leq i\leq h$. Kiss et al. [‘Groups, partitions and representation functions’, Publ. Math. Debrecen85(3) (2014), 425–433] proved that (a) if 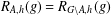$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all 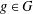$g\in G$, then 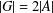$|G|=2|A|$, and (b) if 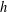$h$ is even and 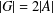$|G|=2|A|$, then 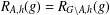$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all 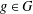$g\in G$. We prove that 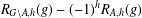$R_{G\setminus A,h}(g)-(-1)^{h}R_{A,h}(g)$ does not depend on 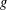$g$. In particular, if 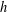$h$ is even and 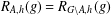$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for some 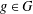$g\in G$, then 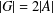$|G|=2|A|$. If 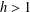$h>1$ is odd and 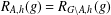$R_{A,h}(g)=R_{G\setminus A,h}(g)$ for all 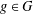$g\in G$, then 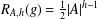$R_{A,h}(g)=\frac{1}{2}|A|^{h-1}$ for all 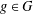$g\in G$. If 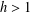$h>1$ is odd and 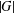$|G|$ is even, then there exists a subset 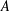$A$ of 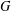$G$ with 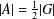$|A|=\frac{1}{2}|G|$ such that 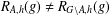$R_{A,h}(g)\not =R_{G\setminus A,h}(g)$ for all 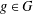$g\in G$.