Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-07T20:22:44.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on the semivariation of vector measures with respect to Banach spaces.

Published online by Cambridge University Press:  17 April 2009

Oscar Blasco
Oscar Blasco
Affiliation:
Department of Mathematics, Universitat de Valencia, Burjassot 46100 (Valencia), Spain, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 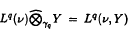and 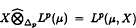. It is shown that any Lp(µ)-valued measure has finite L2(v)-semivariation with respect to the tensor norm 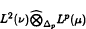for 1 ≤ p < ∞ and finite Lq(v)-semivariation with respect to the tensor norm 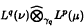whenever either q = 2 and 1 ≤ p ≤ 2 or q > max{p, 2}. However there exist measures with infinite Lq-semivariation with respect to the tensor norm 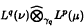for any 1 ≤ q < 2. It is also shown that the measure m (A) = χA has infinite Lq-semivariation with respect to the tensor norm 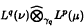if q < p.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 75 , Issue 3 , June 2007 , pp. 469 - 480
Copyright
Copyright © Australian Mathematical Society 2007

References

[1] 1Arregui, J.L. and Blasco, O., ‘(p, q)-summing sequences’, J. Math. Anal. Appl. 247 (2002), 812–827.CrossRefGoogle Scholar
[2]Bartle, R., ‘A general bilinear vector integral’, Studia Math. 15 (1956), 337–351.CrossRefGoogle Scholar
[3]Blasco, O. and Gregori, P., ‘Lorentz spaces of vector-valued measures’, J. London Math. Soc. 67 (2003), 739–751.CrossRefGoogle Scholar
[4]Dinculeanu, N., Vector measures, International Series of Monographs in Pure and Applied Mathematics 95 (Pergamon Press, Oxford, New York, Toronto, 1967).Google Scholar
[5]Diestel, J., Jarchow, H. and Tonge, A., Absolutely summing operators (Cambridge Univ. Press, Cambridge, 1995).CrossRefGoogle Scholar
[6]Diestel, J. and Uhl, J.J., Vector measures, Math. Surveys 15 (Amer. Math. Soc., Providence, R.I., 1997).Google Scholar
[7]Jefferies, B. and Okada, S., ‘Bilinear integration in tensor products’, Rocky Mountain J. Math. 28 (1998), 517–545.CrossRefGoogle Scholar
[8]Jefferies, B. and Okada, S., ‘Semivariation in L p-spaces’, Comment. Math. Univ. Carolin. 44 (2005), 425–436.Google Scholar
[9]Jefferies, B., Okada, S. and Rodrigues-Piazza, L., ‘L p-valued measures without finite X-semivariation for 2 < p < ∞ ’, (preprint).Google Scholar