Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sato, Shuichi
2000.
Proceedings of the Second ISAAC Congress.
Vol. 7,
Issue. ,
p.
83.
Fan, Dashan
and
Sato, Shuichi
2001.
Weak type $(1,1)$ estimates for Marcinkiewicz integrals with rough kernels.
Tohoku Mathematical Journal,
Vol. 53,
Issue. 2,
Chen, Chang-Pao
Fan, Dashan
and
Sato, Shuichi
2002.
deLeeuw’s theorem on Littlewood-Paley functions.
Nagoya Mathematical Journal,
Vol. 165,
Issue. ,
p.
23.
Al-Qassem, H.M.
and
Al-Salman, A.J.
2003.
A note on Marcinkiewicz integral operators.
Journal of Mathematical Analysis and Applications,
Vol. 282,
Issue. 2,
p.
698.
Sato, Shuichi
2003.
Some weighted estimates for Littlewood–Paley functions and radial multipliers.
Journal of Mathematical Analysis and Applications,
Vol. 278,
Issue. 2,
p.
308.
Al-Qassem, H. M.
2004.
Lp estimates for rough parametric Marcinkiewicz integrals.
SUT Journal of Mathematics,
Vol. 40,
Issue. 2,
Wu, Huoxiong
2006.
BOUNDEDNESS OF MULTIPLE MARCINKIEWICZ INTEGRAL OPERATORS WITH ROUGH KERNELS.
Journal of the Korean Mathematical Society,
Vol. 43,
Issue. 3,
p.
635.
Wu, Huoxiong
2006.
Lp estimates for the commutators of Marcinkiewicz integrals with kernels belonging to certain block spaces.
Mathematische Nachrichten,
Vol. 279,
Issue. 9-10,
p.
1128.
Al-Qassem, H. M.
2006.
On weighted inequalities for parametric Marcinkiewicz integrals.
Journal of Inequalities and Applications,
Vol. 2006,
Issue. ,
p.
1.
Wu, Huoxiong
2007.
A rough multiple Marcinkiewicz integral along continuous surfaces.
Tohoku Mathematical Journal,
Vol. 59,
Issue. 2,
Al-Qassem, Hussain Mohammed
2007.
WEIGHTED ESTIMATES FOR ROUGH PARAMETRIC MARCINKIEWICZ INTEGRALS.
Journal of the Korean Mathematical Society,
Vol. 44,
Issue. 6,
p.
1255.
Lu, Shanzhen
2008.
Marcinkiewicz integral with rough kernels.
Frontiers of Mathematics in China,
Vol. 3,
Issue. 1,
p.
1.
Al-Salman, Ahmad
2011.
Parabolic Marcinkiewicz integrals along surfaces on product domains.
Acta Mathematica Sinica, English Series,
Vol. 27,
Issue. 1,
p.
1.
Duoandikoetxea, Javier
2013.
Sharp $$L^p$$ boundedness for a class of square functions.
Revista Matemática Complutense,
Vol. 26,
Issue. 2,
p.
535.
Sato, Shuichi
2014.
Littlewood–Paley operators and Sobolev spaces.
Illinois Journal of Mathematics,
Vol. 58,
Issue. 4,
Shi, Xian-liang
and
Sun, Jie
2015.
Boundedness of parammetric Marcinkiewicz integrals on weighted hardy spaces.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 30,
Issue. 3,
p.
253.
Hart, Jarod
and
Oliveira, Lucas
2017.
Hardy space estimates for limited ranges of Muckenhoupt weights.
Advances in Mathematics,
Vol. 313,
Issue. ,
p.
803.
Sato , Shuichi
2017.
Littlewood–Paley Equivalence and Homogeneous Fourier Multipliers.
Integral Equations and Operator Theory,
Vol. 87,
Issue. 1,
p.
15.
Sato, Shuichi
2017.
Spherical square functions of Marcinkiewicz type with Riesz potentials.
Archiv der Mathematik,
Vol. 108,
Issue. 4,
p.
415.
Al-Qassem, H.
Cheng, L.
and
Pan, Y.
2018.
On generalized Littlewood–Paley functions.
Collectanea Mathematica,
Vol. 69,
Issue. 2,
p.
297.


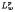 , 1 <
, 1 < 