Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T17:19:02.014Z Has data issue: false hasContentIssue false
  • English
  • Français

A REMARK ON THE STABLE REAL FORMS OF COMPLEX VECTOR BUNDLES OVER MANIFOLDS

Part of: Topological $K$-theory

Published online by Cambridge University Press:  13 March 2017

HUIJUN YANG
HUIJUN YANG*
Affiliation:
School of Mathematics and Statistics, Henan University, Kaifeng 475004, Henan, China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 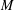$M$ be an $n$-dimensional closed oriented smooth manifold with 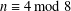$n\equiv 4\;\text{mod}\;8$, and 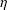$\unicode[STIX]{x1D702}$ be a complex vector bundle over 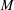$M$. We determine the final obstruction for 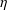$\unicode[STIX]{x1D702}$ to admit a stable real form in terms of the characteristic classes of 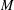$M$ and 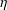$\unicode[STIX]{x1D702}$. As an application, we obtain the criteria to determine which complex vector bundles over a simply connected four-dimensional manifold admit a stable real form.

Keywords

stable real formcomplexificationdifferentiable Riemann–Roch theoremAtiyah–Hirzebruch spectral sequence

MSC classification

Primary: 19L64: Computations, geometric applications
Secondary: 19L10: Riemann-Roch theorems, Chern characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 69 - 76
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Atiyah, M. F. and Hirzebruch, F., ‘Riemann–Roch theorems for differentiable manifolds’, Bull. Amer. Math. Soc. 65 (1959), 276–281.CrossRefGoogle Scholar
Bott, R., ‘The stable homotopy of the classical groups’, Ann. of Math. (2) 70 (1959), 313–337.CrossRefGoogle Scholar
Bott, R., Lectures on K (X), Mathematics Lecture Note Series (W.A. Benjamin, New York, 1969).Google Scholar
Fujii, M., ‘ K O -groups of projective spaces’, Osaka J. Math. 4 (1967), 141–149.Google Scholar
Hilton, P., General Cohomology Theory and K-theory, London Mathematical Society Lecture Note Series, 1 (Cambridge University Press, London, 1971).CrossRefGoogle Scholar
Kulkarni, R. S., ‘On complexifications of differentiable manifolds’, Invent. Math. 44(1) (1978), 46–64.CrossRefGoogle Scholar
Lawson, H. B. and Michelsohn, M.-L., Spin Geometry, Princeton Mathematical Series, 38 (Princeton University Press, Princeton, NJ, 1989).Google Scholar
Milnor, J. W. and Stasheff, J. D., Characteristic Classes, Annals of Mathematics Studies, 76 (Princeton University Press, Princeton, NJ, 1974).CrossRefGoogle Scholar
Mimura, M. and Toda, H., Topology of Lie Groups. I, II, Translations of Mathematical Monographs, 91 (American Mathematical Society, Providence, RI, 1991).Google Scholar
Switzer, R. M., Algebraic Topology – Homotopy and Homology, Classics in Mathematics (Springer, Berlin, 2002).Google Scholar
Totaro, B., ‘Complexifications of nonnegatively curved manifolds’, J. Eur. Math. Soc. 5(1) (2003), 69–94.CrossRefGoogle Scholar
Wall, C. T. C., ‘Poincaré complexes. I’, Ann. of Math. (2) 86 (1967), 213–245.CrossRefGoogle Scholar
Yang, H., ‘A note on stable complex structures on real vector bundles over manifolds’, Topology Appl. 189 (2015), 1–9.CrossRefGoogle Scholar