Published online by Cambridge University Press: 17 April 2009
Two consequences of a theorem of Dahlberg are derived. Let f be a holomorphic function in the unit disk D of the complex plane, and let E be an Fσ subset of the unit circle T. Suppose that 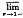 |f(rw)| ≤ M, ω ∈ T/E, for some constant M.
|f(rw)| ≤ M, ω ∈ T/E, for some constant M.
Then f is bounded in either of the two cases:
(i) if f is in the Bloch space and E is of zero measure with respect to the Hausdorff measure associated with the function ψ(t) = t log log (2πee/t),
(ii) if f is integrable with respect to the planar Lebesgue measure on D and E is of zero measure with respect to the Hausdorff measure associated with the function ψ(t) = t log(2πee/t).