No CrossRef data available.
Article contents
REIDEMEISTER’S THEOREM USING TRANSVERSALITY
Published online by Cambridge University Press: 14 October 2024
Abstract
We recover Reidemeister’s theorem using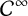 
$\mathcal {C}^{\infty }$ functions and transversality.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 101064705.
References
Alexander, J. W. and Briggs, G. B., ‘On types of knotted curves’, Ann. of Math. (2) 28 (1926–1927), 562–586.CrossRefGoogle Scholar
Baez, J. C. and Langford, L., ‘2-tangles’, Lett. Math. Phys. 43 (1998), 187–197.CrossRefGoogle Scholar
Carter, J. S., Rieger, J. H. and Saito, M., ‘A combinatorial description of knotted surfaces and their isotopies’, Adv. Math. 127(1) (1997), 1–51.CrossRefGoogle Scholar
Carter, J. S. and Saito, M., ‘Reidemeister moves for surface isotopies and their interpretation as moves to movies’, J. Knot Theory Ramifications 2(3) (1993), 251–284.CrossRefGoogle Scholar
Carter, J. S. and Saito, M., Knotted Surfaces and Their Diagrams, Mathematical Surveys and Monographs, 55 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Fischer, J. E. Jr, ‘2-categories and 2-knots’, Duke Math. J. 75(2) (1994), 493–526.CrossRefGoogle Scholar
Golubitsky, M. and Guillemin, V., Stable Mappings and Their Singularities, Graduate Texts in Mathematics, 14 (Springer, New York, 2012).Google Scholar
Kauffman, L. H., ‘Invariants of graphs in three-space’, Trans. Amer. Math. Soc. 311(2) (1989), 697–710.CrossRefGoogle Scholar
Laudenbach, F., ‘Transversalité de Thom et
$h$
-principe de Gromov’, Lecture notes from a lecture series at the University of Ouargla (2013). Available online at https://www.math.sciences.univ-nantes.fr/~laudenba/cours_ouargla3.pdf.Google Scholar
$h$
-principe de Gromov’, Lecture notes from a lecture series at the University of Ouargla (2013). Available online at https://www.math.sciences.univ-nantes.fr/~laudenba/cours_ouargla3.pdf.Google ScholarLaudenbach, F., ‘A proof of Reidemeister–Singer’s theorem by Cerf’s methods’, Ann. Fac. Sci. Toulouse Math. (6) 23(1) (2014), 197–221.CrossRefGoogle Scholar
Mather, J. N., ‘Stability of
${C}^{\infty }$
mappings: V, transversality’, Adv. Math. 4(3) (1970), 301–336.CrossRefGoogle Scholar
${C}^{\infty }$
mappings: V, transversality’, Adv. Math. 4(3) (1970), 301–336.CrossRefGoogle ScholarMiller, K. A., Singularity Theory for Extended Ccobordism Categories and an Application to Graph Theory, PhD Thesis (University of California, Berkeley, 2022).Google Scholar
Ozsváth, P. S., Stipsicz, A. I. and Szabó, Z.. Grid Homology for Knots and Links, Mathematical Surveys and Monographs, 208 (American Mathematical Society, Providence, RI, 2015).CrossRefGoogle Scholar
Queffelec, H. and Walker, K., ‘Movie moves for framed foams from multijet transversality’, Quantum Topol., to appear. Published online (27 February 2024); Preprint, 2024, arXiv:2205.14947, 79 pages.CrossRefGoogle Scholar
Reidemeister, K., ‘Elementare Begründung der Knotentheorie’, Abh. Math. Semin. Univ. Hambg. 5 (1927), 24–32.CrossRefGoogle Scholar
Roseman, D., ‘Elementary moves for higher dimensional knots’, Fund. Math. 184 (2004), 291–310.CrossRefGoogle Scholar
Thom, R., ‘Quelques propriétés globales des variétés différentiables’, Comment. Math. Helv. 28(1) (1954), 17–86.CrossRefGoogle Scholar
Thom, R., ‘Les singularités des applications différentiables’, Ann. Inst. Fourier (Grenoble) 6 (1956), 43–87.CrossRefGoogle Scholar