No CrossRef data available.
Published online by Cambridge University Press: 19 September 2022
For a simple bipartite graph G, we give an upper bound for the regularity of powers of the edge ideal
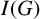 $I(G)$
in terms of its vertex domination number. Consequently, we explicitly compute the regularity of powers of the edge ideal of a bipartite Kneser graph. Further, we compute the induced matching number of a bipartite Kneser graph.
$I(G)$
in terms of its vertex domination number. Consequently, we explicitly compute the regularity of powers of the edge ideal of a bipartite Kneser graph. Further, we compute the induced matching number of a bipartite Kneser graph.