Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T21:40:03.206Z Has data issue: false hasContentIssue false
  • English
  • Français

REGULAR ORBITS OF COPRIME LINEAR GROUPS IN LARGE CHARACTERISTIC

Part of: Linear algebraic groups and related topics Representation theory of groups

Published online by Cambridge University Press:  02 May 2017

BENJAMIN SAMBALE Open the ORCID record for BENJAMIN SAMBALE [Opens in a new window]
BENJAMIN SAMBALE*
Affiliation:
Fachbereich Mathematik, TU Kaiserslautern, 67653 Kaiserslautern, Germany email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that a finite coprime linear group 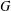$G$ in characteristic 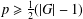$p\geq \frac{1}{2}(|G|-1)$ has a regular orbit. This bound on 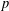$p$ is best possible. We also give an application to blocks with abelian defect groups.

Keywords

coprime linear groupsregular orbitsminimal subgroups

MSC classification

Primary: 20G40: Linear algebraic groups over finite fields
Secondary: 20C15: Ordinary representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 438 - 444
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Berkovich, Y., Groups of Prime Power Order, Vol. 1, de Gruyter Expositions in Mathematics, 46 (Walter de Gruyter, Berlin, 2008).Google Scholar
Burness, T. C. and Scott, S. D., ‘On the number of prime order subgroups of finite groups’, J. Aust. Math. Soc. 87 (2009), 329–357.Google Scholar
Espuelas, A., ‘The existence of regular orbits’, J. Algebra 127 (1989), 259–268.CrossRefGoogle Scholar
Fleischmann, P., ‘Finite groups with regular orbits on vector spaces’, J. Algebra 103 (1986), 211–215.CrossRefGoogle Scholar
The GAP Group, GAP—Groups, Algorithms, and Programming, Version 4.8.6, 2016,http://www.gap-system.org.Google Scholar
Halasi, Z. and Podoski, K., ‘Every coprime linear group admits a base of size two’, Trans. Amer. Math. Soc. 368 (2016), 5857–5887.Google Scholar
Hargraves, B. B., ‘The existence of regular orbits for nilpotent groups’, J. Algebra 72 (1981), 54–100.CrossRefGoogle Scholar
Hartley, B. and Turull, A., ‘On characters of coprime operator groups and the Glauberman character correspondence’, J. reine angew. Math. 451 (1994), 175–219.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (AMS Chelsea, Providence, RI, 2006).Google Scholar
Köhler, C. and Pahlings, H., ‘Regular orbits and the k (GV)-problem’, in: Groups and Computation, III (Columbus, OH, 1999), Ohio State University Mathematics Research Institute Publications, 8 (de Gruyter, Berlin, 2001), 209–228.Google Scholar
Robinson, G. R., ‘On Brauer’s k (B) problem’, J. Algebra 147 (1992), 450–455.Google Scholar
Sambale, B., Blocks of Finite Groups and Their Invariants, Springer Lecture Notes in Mathematics, 2127 (Springer, Cham, 2014).Google Scholar
Sambale, B., ‘On the Brauer–Feit bound for abelian defect groups’, Math. Z. 276 (2014), 785–797.Google Scholar
Sambale, B., ‘Cartan matrices and Brauer’s k (B)-conjecture IV’, J. Math. Soc. Japan 69 (2017), 1–20.Google Scholar
Sambale, B., ‘On blocks with abelian defect groups of small rank’, Results Math. 71 (2017), 411–422.Google Scholar
Schmid, P., The Solution of the k (GV) Problem, ICP Advanced Texts in Mathematics, 4 (Imperial College Press, London, 2007).Google Scholar
Yang, Y., ‘Regular orbits of nilpotent subgroups of solvable linear groups’, J. Algebra 325 (2011), 56–69.Google Scholar