Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-08T09:58:11.978Z Has data issue: false hasContentIssue false
  • English
  • Français

THE REGULAR GRAPH OF A NONCOMMUTATIVE RING

Published online by Cambridge University Press:  13 February 2013

S. AKBARI  and
F. HEYDARI
S. AKBARI*
Affiliation:
Department of Mathematical Sciences, Sharif University of Technology, Tehran, Iran
F. HEYDARI
Affiliation:
Department of Mathematics, Karaj Branch, Islamic Azad University, Karaj, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 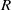$R$ be a ring and 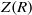$Z(R)$ be the set of all zero-divisors of 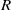$R$. The total graph of 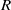$R$, denoted by 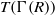$T(\Gamma (R))$ is a graph with all elements of 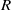$R$ as vertices, and two distinct vertices 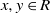$x, y\in R$ are adjacent if and only if 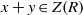$x+ y\in Z(R)$. Let the regular graph of 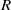$R$, 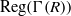$\mathrm{Reg} (\Gamma (R))$, be the induced subgraph of 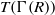$T(\Gamma (R))$ on the regular elements of 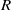$R$. In 2008, Anderson and Badawi proved that the girth of the total graph and the regular graph of a commutative ring are contained in the set 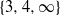$\{ 3, 4, \infty \} $. In this paper, we extend this result to an arbitrary ring (not necessarily commutative). We also prove that if 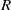$R$ is a reduced left Noetherian ring and 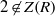$2\not\in Z(R)$, then the chromatic number and the clique number of 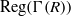$\mathrm{Reg} (\Gamma (R))$ are the same and they are 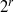${2}^{r} $, where $r$ is the number of minimal prime ideals of 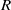$R$. Among other results, we show that if 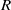$R$ is a semiprime left Noetherian ring and 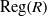$\mathrm{Reg} (R)$ is finite, then 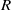$R$ is finite.

Keywords

regular graphtotal graphgirthchromatic number
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 132 - 140
Copyright
©2013 Australian Mathematical Publishing Association Inc. 

References

Afkhami, M., Karimi, M. and Khashyarmanesh, K., On the regular digraph of ideals of commutative rings, Bull. Aust. Math. Soc., to appear.Google Scholar
Akbari, S., Kiani, D., Mohammadi, F. and Moradi, S, ‘The total graph and regular graph of a commutative ring’, J. Pure Appl. Algebra 213 (2009), 2224–2228.Google Scholar
Alfaro, R. and Kelarev, A. V., ‘Recent results on ring constructions for error-correcting codes, algebraic structures and their representations’, Contemp. Math. 376 (2005), 1–12.Google Scholar
Anderson, D. F. and Badawi, A., ‘The total graph of a commutative ring’, J. Algebra 320 (2008), 2706–2719.CrossRefGoogle Scholar
Ganesan, N., ‘Properties of rings with a finite number of zero-divisors II’, Math. Ann. 161 (1965), 241–246.Google Scholar
Gao, D. Y., Kelarev, A. V. and Yearwood, J. L., ‘Optimization of matrix semirings for classification systems’, Bull. Aust. Math. Soc. 84 (2011), 492–503.Google Scholar
Goodearl, K. R. and Warfield, R. B. Jr, An Introduction to Noncommutative Noetherian Rings (Cambridge University Press, Cambridge, 2004).Google Scholar
Herstein, I. N., ‘A counterexample in Noetherian rings’, Proc. Natl. Acad. Sci. USA. 54 (1965), 1036–1037.CrossRefGoogle ScholarPubMed
Kelarev, A. V., Ring Constructions and Applications (World Scientific, River Edge, NJ, 2002).Google Scholar
Kelarev, A. V. and Passman, D. S., ‘A description of incidence rings of group automata’, Contemp. Math. 456 (2008), 27–33.CrossRefGoogle Scholar
Kelarev, A., Ryan, J. and Yearwood, J., ‘Cayley graphs as classifiers for data mining: the influence of asymmetries’, Discrete Math. 309 (17) (2009), 5360–5369.Google Scholar
Kelarev, A. V., Yearwood, J. L. and Vamplew, P. W., ‘A polynomial ring construction for classification of data’, Bull. Aust. Math. Soc. 79 (2009), 213–225.Google Scholar
Lam, T. Y., A First Course in Noncommutative Rings (Springer, Berlin, 1991).Google Scholar
Lam, T. Y., Lectures on Modules and Rings (Springer, Berlin, 1998).Google Scholar
McConnell, J. C. and Robson, J. C., Noncommutative Noetherian Rings, revised edition, Graduate Studies in Mathematics, 30 (American Mathematical Society, Providence, RI, 2001).Google Scholar
Moconja, S. M. and Petrović, Z. Z., ‘On the structure of comaximal graphs of commutative rings with identity’, Bull. Aust. Math. Soc. 83 (1) (2011), 11–21.CrossRefGoogle Scholar
Raghavendran, R., ‘A class of finite rings’, Compositio Math. 22 (1970), 49–57.Google Scholar
Rowen, L. H., Ring Theory, Vol. I (Academic Press, Boston, 1988).Google Scholar
Stewart, I., ‘Finite rings with a specified group of units’, Math. Z. 126 (1972), 51–58.Google Scholar