Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T07:20:18.467Z Has data issue: false hasContentIssue false
  • English
  • Français

REGULAR CONGRUENCES ON AN IDEMPOTENT-REGULAR-SURJECTIVE SEMIGROUP

Part of: Lattices Semigroups

Published online by Cambridge University Press:  30 July 2013

ROMAN S. GIGOŃ
ROMAN S. GIGOŃ*
Affiliation:
Institute of Mathematics and Computer Science, Wroclaw University of Technology, Wyb. Wyspianskiego 27, 50-370 Wroclaw, Poland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A semigroup 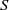$S$ is called idempotent-surjective (respectively, regular-surjective) if whenever 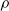$\rho $ is a congruence on 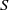$S$ and 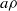$a\rho $ is idempotent (respectively, regular) in 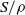$S/ \rho $, then there is 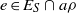$e\in {E}_{S} \cap a\rho $ (respectively, 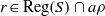$r\in \mathrm{Reg} (S)\cap a\rho $), where 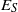${E}_{S} $ (respectively, 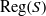$\mathrm{Reg} (S)$) denotes the set of all idempotents (respectively, regular elements) of 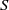$S$. Moreover, a semigroup 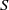$S$ is said to be idempotent-regular-surjective if it is both idempotent-surjective and regular-surjective. We show that any regular congruence on an idempotent-regular-surjective (respectively, regular-surjective) semigroup is uniquely determined by its kernel and trace (respectively, the set of equivalence classes containing idempotents). Finally, we prove that all structurally regular semigroups are idempotent-regular-surjective.

Keywords

semigroupregular congruenceregular-surjective semigroupidempotent-surjective semigroupstructurally regular semigroupkerneltrace

MSC classification

Secondary: 20M99: None of the above, but in this section 06B10: Ideals, congruence relations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 190 - 196
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, Vol. I, Mathematical Surveys, 7 (American Mathematical Society, Providence, RI, 1961).CrossRefGoogle Scholar
Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, Vol. II, Mathematical Surveys, 7 (American Mathematical Society, Providence, RI, 1967).CrossRefGoogle Scholar
Edwards, P. M., ‘Eventually regular semigroups’, Bull. Aust. Math. Soc. 28 (1983), 23–38.CrossRefGoogle Scholar
Gigoń, R. S., ‘On the lattice of congruences on idempotent-regular-surjective semigroups’, Comm. Algebra, to appear.Google Scholar
Kopamu, S. J. L., ‘On semigroup species’, Comm. Algebra 23 (1995), 5513–5537.CrossRefGoogle Scholar
Kopamu, S. J. L., ‘The concept of structural regularity’, Port. Math. 53 (1996), 435–456.Google Scholar
Luo, Y., Fan, X. and Li, X., ‘Regular congruences on an E-inversive semigroup’, Semigroup Forum 76 (2008), 354–363.CrossRefGoogle Scholar
Mitsch, H. and Petrich, M., ‘Basic properties on E-inversive semigroups’, Comm. Algebra 28 (2000), 5169–5182.CrossRefGoogle Scholar
Shao, F. and He, Y., ‘Partial kernel normal systems for eventually regular semigroups’, Semigroup Forum 71 (2005), 401–410.CrossRefGoogle Scholar