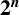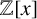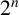Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gaál, István
2024.
Monogenity and Power Integral Bases: Recent Developments.
Axioms,
Vol. 13,
Issue. 7,
p.
429.
Jones, Lenny
2024.
Reciprocal Monogenic Septinomials of Degree 2n3.
Annales Mathematicae Silesianae,
Vol. 0,
Issue. 0,
Jones, Lenny
2025.
The monogenicity and Galois groups of certain reciprocal quintinomials.
Functiones et Approximatio Commentarii Mathematici,
Vol. -1,
Issue. -1,