Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Graham, Ian
Hamada, Hidetaka
and
Kohr, Gabriela
2006.
Radius problems for holomorphic mappings on the unit ball in Cn.
Mathematische Nachrichten,
Vol. 279,
Issue. 13-14,
p.
1474.
Ponnusamy, S.
and
Qiao, J.
2013.
Polynomial approximation of certain biharmonic mappings.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 81,
Issue. ,
p.
149.
Ahuja, Om P.
Nagpal, Sumit
and
Ravichandran, V.
2014.
Radius Constants for Functions with the Prescribed Coefficient Bounds.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Nargesi, Mahnaz M.
Ali, Rosihan M.
and
Ravichandran, V.
2014.
Radius Constants for Analytic Functions with Fixed Second Coefficient.
The Scientific World Journal,
Vol. 2014,
Issue. ,
p.
1.
MENDIRATTA, RAJNI
NAGPAL, SUMIT
and
RAVICHANDRAN, V.
2015.
Radii of Starlikeness and Convexity for Analytic Functions with Fixed Second Coefficient Satisfying Certain Coefficient Inequalities.
Kyungpook mathematical journal,
Vol. 55,
Issue. 2,
p.
395.
Yahya, Abdullah
and
Soh, Shaharuddin Cik
2017.
Radius of convexity of a certain class of close-to-convex functions.
Vol. 1905,
Issue. ,
p.
030040.
Righetti, Mattia
2017.
On the density of zeros of linear combinations of Euler products for σ > 1.
Algebra & Number Theory,
Vol. 11,
Issue. 9,
p.
2131.
Hu, Zhenyong
Srivastava, H. M.
and
Zhang, Ying
2024.
Sharp starlike and convex radius for the differential operator of analytic functions.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 76,
Issue. 10,
p.
1455.


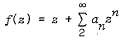 be regular in the disk |z| < 1. The radius of univalence 0.164 … of the family of f with |a
be regular in the disk |z| < 1. The radius of univalence 0.164 … of the family of f with |a