Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T01:19:48.349Z Has data issue: false hasContentIssue false
  • English
  • Français

Radial growth and boundedness for Bloch functions

Published online by Cambridge University Press:  17 April 2009

A. Bonilla  and
F. Perez Gonzalez
A. Bonilla
Affiliation:
Departamento de Análisis Matemático Facultad de Matemáticas, Universidad de La Laguna, 38271 La Laguna, Tenerife, Spain
F. Perez Gonzalez
Affiliation:
Departamento de Análisis Matemático Facultad de Matemáticas, Universidad de La Laguna, 38271 La Laguna, Tenerife, Spain
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B be the Bloch space of all those functions f holomorphic in the open unit disc D of the complex plane satisfying 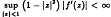. We establish sufficient conditions for the boundedness of functions f belonging to B satisfying a certain uniform radial boundedness condition, and, by introducing a wide class of subsets E of ∂D, which we call negligible sets for boundedness, we show that if f ∈ B and there is a constant K > 0 such that 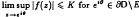, then f is bounded in D. Hence a significant extension of a theorem of Goolsby is obtained.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 42 , Issue 1 , August 1990 , pp. 33 - 39
Copyright
Copyright © Australian Mathematical Society 1990

References

[l]Anderson, J.M., Clunie, J. and Pommerenke, C., ‘On Bloch functions and normal functions’, J. Reine. Angew. Math. 270 (1974), 12–37.Google Scholar
[2]Cima, J.A., ‘The basic properties of Bloch functions’, Internal. J. Math. Math. Sci. 2–3 (1979), 369–413.CrossRefGoogle Scholar
[3]Dahlberg, B.E.I., ‘On the radial boundary values of subharmonic functions’, Math. Scand. 40 (1977), 301–317.CrossRefGoogle Scholar
[4]Girela, D., ‘Integral means and radial growth of Bloch functions’, Math. Z. 195 (1987), 37–50.CrossRefGoogle Scholar
[5]Goolsby, R.C., ‘Boundedness for Bloch functions’, Rocky Mountain J. Math. 16 (1986), 717–726.CrossRefGoogle Scholar
[6]Korenblum, B., ‘Estimates and radial growth of Bloch functions’, Bull. Amer. Math. Soc. (N.S.) 12 (1985), 99–102.CrossRefGoogle Scholar
[7]Lehto, O. and Virtanen, K.I., ‘Boundary behaviour and normal meromorphic functions’, Acta Math. 97 (1957), 47–65.CrossRefGoogle Scholar
[8]Makarov, N.G., ‘On the distortion of boundary sets under conformal mappings’, Proc. London Math. Soc. 51 (1985), 369–384.CrossRefGoogle Scholar