Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chattopadhyay, Jaitra
Roy, Bidisha
and
Sarkar, Subha
2019.
On fractionally dense sets.
Rocky Mountain Journal of Mathematics,
Vol. 49,
Issue. 3,
Donnay, Christopher
Garcia, Stephan Ramon
and
Rouse, Jeremy
2019.
p-adic quotient sets II: Quadratic forms.
Journal of Number Theory,
Vol. 201,
Issue. ,
p.
23.
Miska, Piotr
Murru, Nadir
and
Sanna, Carlo
2019.
On the p-adic denseness of the quotient set of a polynomial image.
Journal of Number Theory,
Vol. 197,
Issue. ,
p.
218.
Miska, Piotr
and
Sanna, Carlo
2020.
p-Adic Denseness of Members of Partitions of $$\pmb {\mathbb {N}}$$N and Their Ratio Sets.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 43,
Issue. 2,
p.
1127.
Garcia, Stephan Ramon
2020.
A Project-Based Guide to Undergraduate Research in Mathematics.
p.
203.
LEONETTI, PAOLO
and
SANNA, CARLO
2020.
DIRECTIONS SETS: A GENERALISATION OF RATIO SETS.
Bulletin of the Australian Mathematical Society,
Vol. 101,
Issue. 3,
p.
389.
Miska, Piotr
2021.
A note on p-adic denseness of quotients of values of quadratic forms.
Indagationes Mathematicae,
Vol. 32,
Issue. 3,
p.
639.
Antony, Deepa
Barman, Rupam
and
Miska, Piotr
2022.
p-adic quotient sets: diagonal forms.
Archiv der Mathematik,
Vol. 119,
Issue. 5,
p.
461.
Antony, Deepa
and
Barman, Rupam
2022.
p-adic quotient sets: cubic forms.
Archiv der Mathematik,
Vol. 118,
Issue. 2,
p.
143.
ANTONY, DEEPA
and
BARMAN, RUPAM
2023.
-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 1,
p.
19.
Antony, Deepa
and
Barman, Rupam
2025.
p-Adic quotient sets: Linear recurrence sequences with reducible characteristic polynomials.
Canadian Mathematical Bulletin,
Vol. 68,
Issue. 1,
p.
177.
Kumar, Rishi
2025.
Kepler sets of second-order linear recurrence sequences over Qp.
International Journal of Number Theory,
Vol. 21,
Issue. 01,
p.
75.
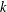 $k$-GENERALISED FIBONACCI NUMBERS IS DENSE IN
$k$-GENERALISED FIBONACCI NUMBERS IS DENSE IN 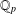 $\mathbb{Q}_{p}$
$\mathbb{Q}_{p}$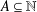 $A\subseteq \mathbb{N}$ is defined as
$A\subseteq \mathbb{N}$ is defined as 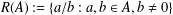 $R(A):=\{a/b:a,b\in A,b\neq 0\}$. Using algebraic number theory in
$R(A):=\{a/b:a,b\in A,b\neq 0\}$. Using algebraic number theory in 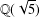 $\mathbb{Q}(\sqrt{5})$, Garcia and Luca [‘Quotients of Fibonacci numbers’, Amer. Math. Monthly, to appear] proved that the quotient set of Fibonacci numbers is dense in the
$\mathbb{Q}(\sqrt{5})$, Garcia and Luca [‘Quotients of Fibonacci numbers’, Amer. Math. Monthly, to appear] proved that the quotient set of Fibonacci numbers is dense in the 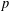 $p$-adic numbers
$p$-adic numbers 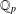 $\mathbb{Q}_{p}$ for all prime numbers
$\mathbb{Q}_{p}$ for all prime numbers 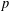 $p$. For any integer
$p$. For any integer 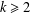 $k\geq 2$, let
$k\geq 2$, let 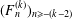 $(F_{n}^{(k)})_{n\geq -(k-2)}$ be the sequence of
$(F_{n}^{(k)})_{n\geq -(k-2)}$ be the sequence of 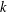 $k$-generalised Fibonacci numbers, defined by the initial values
$k$-generalised Fibonacci numbers, defined by the initial values 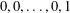 $0,0,\ldots ,0,1$ (
$0,0,\ldots ,0,1$ (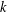 $k$ terms) and such that each successive term is the sum of the
$k$ terms) and such that each successive term is the sum of the 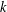 $k$ preceding terms. We use
$k$ preceding terms. We use 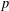 $p$-adic analysis to generalise the result of Garcia and Luca, by proving that the quotient set of
$p$-adic analysis to generalise the result of Garcia and Luca, by proving that the quotient set of 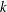 $k$-generalised Fibonacci numbers is dense in
$k$-generalised Fibonacci numbers is dense in 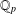 $\mathbb{Q}_{p}$ for any integer
$\mathbb{Q}_{p}$ for any integer 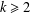 $k\geq 2$ and any prime number
$k\geq 2$ and any prime number 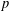 $p$.
$p$.