Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T14:52:40.372Z Has data issue: false hasContentIssue false
  • English
  • Français

QUASIHOMOGENEOUS TOEPLITZ OPERATORS WITH INTEGRABLE SYMBOLS ON THE HARMONIC BERGMAN SPACE

Part of: Special classes of linear operators

Published online by Cambridge University Press:  13 June 2014

XING-TANG DONG ,
CONGWEN LIU  and
ZE-HUA ZHOU
XING-TANG DONG
Affiliation:
Department of Mathematics, Tianjin University, Tianjin 300072, PR China email [email protected]
CONGWEN LIU
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, Anhui, PR China Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Science, Beijing 100864, PR China email [email protected]
ZE-HUA ZHOU*
Affiliation:
Department of Mathematics, Tianjin University, Tianjin 300072, PR China Center for Applied Mathematics, Tianjin University, Tianjin 300072, PR China email [email protected], [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we completely determine the commutativity of two Toeplitz operators on the harmonic Bergman space with integrable quasihomogeneous symbols, one of which is of the form 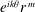$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}e^{ik\theta }r^{\, {m}}$. As an application, the problem of when their product is again a Toeplitz operator is solved. In particular, Toeplitz operators with bounded symbols on the harmonic Bergman space commute with 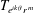$T_{e^{ik\theta }r^{\, {m}}}$ only in trivial cases, which appears quite different from results on analytic Bergman space in Čučković and Rao [‘Mellin transform, monomial symbols, and commuting Toeplitz operators’, J. Funct. Anal.154 (1998), 195–214].

Keywords

Toeplitz operatorsharmonic Bergman spacequasihomogeneous symbols

MSC classification

Secondary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 494 - 503
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Abramowitz, M. and Stegun, I. A. (eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Applied Mathematics Series, 55 (National Bureau of Standards, Washington, 1965), 4th printing with corrections.Google Scholar
Ahern, P. and Čučković, Ž., ‘A theorem of Brown–Halmos type for Bergman space Toeplitz operators’, J. Funct. Anal. 187 (2001), 200–210.Google Scholar
Axler, S. and Čučković, Ž., ‘Commuting Toeplitz operators with harmonic symbols’, Integral Equations Operator Theory 14 (1991), 1–12.Google Scholar
Brown, A. and Halmos, P. R., ‘Algebraic properties of Toeplitz operators’, J. reine angew. Math. 213 (1964), 89–102.Google Scholar
Choe, B. R. and Lee, Y. J., ‘Commuting Toeplitz operators on the harmonic Bergman spaces’, Michigan Math. J. 46 (1999), 163–174.CrossRefGoogle Scholar
Choe, B. R. and Lee, Y. J., ‘Commutants of analytic Toeplitz operators on the harmonic Bergman space’, Integral Equations Operator Theory 50 (2004), 559–564.Google Scholar
Čučković, Ž. and Rao, N. V., ‘Mellin transform, monomial symbols, and commuting Toeplitz operators’, J. Funct. Anal. 154 (1998), 195–214.CrossRefGoogle Scholar
Ding, X. H., ‘A question of Toeplitz operators on the harmonic Bergman space’, J. Math. Anal. Appl. 344 (2008), 367–372.Google Scholar
Dong, X.-T. and Zhou, Z.-H., ‘Products of Toeplitz operators on the harmonic Bergman space’, Proc. Amer. Math. Soc. 138 (2010), 1765–1773.CrossRefGoogle Scholar
Dong, X.-T. and Zhou, Z.-H., ‘Algebraic properties of Toeplitz operators with separately quasihomogeneous symbols on the Bergman space of the unit ball’, J. Operator Theory 66 (2011), 193–207.Google Scholar
Dong, X.-T. and Zhou, Z.-H., ‘Commuting quasihomogeneous Toeplitz operators on the harmonic Bergman space’, Complex Anal. Oper. Theory 7 (2013), 1267–1285.CrossRefGoogle Scholar
Dong, X.-T. and Zhou, Z.-H., ‘Product equivalence of quasihomogeneous Toeplitz operators on the harmonic Bergman space’, Studia Math. 219 (2013), 163–175.CrossRefGoogle Scholar
Gorkin, P. and Zheng, D., ‘Essentially commuting Toeplitz operators’, Pacific J. Math. 190 (1999), 87–109.CrossRefGoogle Scholar
Guo, K. and Zheng, D., ‘Essentially commuting Hankel and Toeplitz operators’, J. Funct. Anal. 201 (2003), 121–147.CrossRefGoogle Scholar
Louhichi, I., ‘Powers and roots of Toeplitz operators’, Proc. Amer. Math. Soc. 135 (2007), 1465–1475.CrossRefGoogle Scholar
Louhichi, I., Strouse, E. and Zakariasy, L., ‘Products of Toeplitz operators on the Bergman space’, Integral Equations Operator Theory 54 (2006), 525–539.CrossRefGoogle Scholar
Louhichi, I. and Zakariasy, L., ‘On Toeplitz operators with quasihomogeneous symbols’, Arch. Math. 85 (2005), 248–257.CrossRefGoogle Scholar
Louhichi, I. and Zakariasy, L., ‘Quasihomogeneous Toeplitz operators on the harmonic Bergman space’, Arch. Math. 98 (2012), 49–60.Google Scholar
Ohno, S., ‘Toeplitz and Hankel operators on the harmonic Bergman spaces’, RIMS Kôkyûroku Bessatsu 946 (1996), 25–34.Google Scholar
Zhou, Z. H. and Dong, X. T., ‘Algebraic properties of Toeplitz operators with radial symbols on the Bergman space of the unit ball’, Integral Equations Operator Theory 64 (2009), 137–154.CrossRefGoogle Scholar