Hostname: page-component-599cfd5f84-d4snv Total loading time: 0 Render date: 2025-01-07T07:13:21.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantised affine algebras and parameter-dependent R-matrices

Published online by Cambridge University Press:  17 April 2009

Anthony J. Bracken ,
Mark D. Gould  and
Yao-Zhong Zhang
Anthony J. Bracken
Affiliation:
Department of MathematicsUniversity of QueenslandQueensland 4072Australia
Mark D. Gould
Affiliation:
Department of MathematicsUniversity of QueenslandQueensland 4072Australia
Yao-Zhong Zhang
Affiliation:
Department of MathematicsUniversity of QueenslandQueensland 4072Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

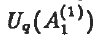Let Uq(G(1)) be a quantised non-twisted affine Lie algebra with Uq(G) the corresponding quantised simple Lie algebra. Using the previously obtained universal R-matrices for and 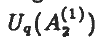, explicitly spectral-dependent universal R-matrices for Uq(A1) and Uq(A2) are determined. These spectral-dependent universal R-matrices are evaluated in some concrete representations; well-known results for the fundamental representations are reproduced, and an explicit formula for the spectral-dependent R-matrix associated with the V(3) ⊗ V(6) module is derived, where V(3) and V(6) carry the 3- and 6-dimensional representations of Uq(A2), respectively.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 51 , Issue 2 , April 1995 , pp. 177 - 194
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Alvarez-Gaumé, L., Gomez, C. and Sierra, G., ‘Quantum group interpretation of some conformal field theories’, Phys. Lett. B, 220 (1989), 142–152.CrossRefGoogle Scholar
[2]Alvarex-Gaumé, L., Gomez, C. and Sierra, G., ‘Hidden quantum symmetries in rational conformal field theories’, Nuclear Phys. B 319 (1989), 155–186.Google Scholar
[3]Babelon, O. and Bonora, L., ‘Conformal affine sl 2 Toda field theory’, Phys. Lett. B 244 (1990), 220–226.Google Scholar
[4]Baxter, R.J., Exactly solved models in statistical mechanics (Academic Press, New York, 1982).Google Scholar
[5]Bracken, A.J., Delius, G.W., Gould, M.D. and Zhang, Y.-Z., ‘Solutions to the (graded) Yang-Baxter equation with extra non-additive parameterst’, J. Phys. A. (to appear).Google Scholar
[6]Bracken, A.J., Delius, G.W., Gould, M.D. and Zhang, Y.-Z., ‘Infinite families of gauge-equivalent R-matrices and gradations of quantized affine algebras’, Internat. J. Modern Phys. (to appear).Google Scholar
[7]Delius, G.W., Gould, M.D. and Zhang, Y.-Z., ‘On the construction of trigonometric solutions of the Yang-Baxter equation’, Nuclear Phys. B (to appear).Google Scholar
[8]Drinfeld, V.G., ‘Quantum groups’, Proc. ICM, Berkeley 1 (1986), 798–820.Google Scholar
[9]Faddeev, L.D., ‘Integrable models in (1+1)-dimensional quantum field theory’, in Recent advances in field theory and statistical mechanics (North-Holland, New York, 1984), pp. 563–608.Google Scholar
[10]Jimbo, M., ‘Aq-difference analogue of U(g) and the Yang-Baxter equation’, Lett. Math. Phys. 10 (1985), 63–69.CrossRefGoogle Scholar
[11]Jimbo, M., ‘A q-analogue of U(gl(N + 1)) Hecke algebra and the Yang-Baxter equation’, Lett. Math. Phys. 11 (1986), 247–252.CrossRefGoogle Scholar
[12]Jimbo, M., ‘Quantum R matrix for the generalized Toda system’, Comm. Math. Phys. 102 (1986), 537–542.CrossRefGoogle Scholar
[13]Jones, V.F.R., ‘Baxterization’, Internal J. Modern Phys. B 4 (1990), 701–713.Google Scholar
[14]Kac, V.G., Infinite dimensional Lie algebras: An introduction (Birkhäuser, Boston, 1983).Google Scholar
[15]Khoroshkin, S.M. and Tolstoy, V.N., ‘The uniqueness theorem for the universal R-matrix’, Lett. Math. Phys. 24 (1992), 231–244.Google Scholar
[16]Khoroshkin, S.M. and Tolstoy, V.N., ‘The universal R-matrix for quantum non-twisted affine Lie algebras’, Funktsional. Anal. i Prilozhen 26 (1992), 85–88.Google Scholar
[17]Kirillov, A.N. and Reshetikhin, N., ‘Representations of the algebra Uq(sl(2)), q-orthogonal polynomials and invariants of links’, preprint LOMI E–9–88.Google Scholar
[18]Links, J.R., Gould, M.D. and Zhang, R.B., ‘Quantum supergroups, link polynomials and representations of the braid generator’, Rev. Math. Phys. 5 (1993), 345–361.Google Scholar
[19]Moore, G. and Reshetikhin, N.Yu., ‘A comment on quantum group symmetry in conformal field theory’, Nuclear Phys. B 328 (1989), 557–574.Google Scholar
[20]Reshetikhin, N., ‘Quantized universal enveloping algebras, the Yang-Baxter equation and inveriants of links: I, II’, preprints LOMI E–4–87, E–17–87.Google Scholar
[21]Toppan, F. and Zhang, Y.-Z., ‘Superconformal affine Lionville theory’, Phys. Lett. B 292 (1992), 67–76.Google Scholar
[22]Wadati, M., Deguchi, T. and Akutsu, Y., ‘Exactly solvable models and knot theory’, Phys. Rep. 180 (1989), 247–332.CrossRefGoogle Scholar
[23]Witten, E., ‘Quantum field theory and the Jones polynomial’, Commun. Math. Phys. 121 (1989), 351–399.Google Scholar
[24]Zhang, R.B., Gould, M.D. and Bracken, A.J., ‘Quantum group invariants and link polynomials’, Commun. Math. Phys. 137 (1991), 13–27.CrossRefGoogle Scholar
[25]Zhang, R.B., Gould, M.D. and Bracken, A.J., ‘From representations of the braid group to solutions of the Yang-Baxter equation’, Nuclear Phys. B 354 (1991), 625–652.Google Scholar
[26]Zhang, Y.-Z. and Gould, M.D., ‘Quantum affine algebras and universal R-matrix with spectral parameter’, Lett. Math. Phys. 31 (1994), 101–110.CrossRefGoogle Scholar
[27]Zhang, Y.-Z. and Gould, M.D., ‘On universal R-matrix for quantized nontwisted rank 3 affine KM algebras’, Lett. Math. Phys. 29 (1993), 19–31.CrossRefGoogle Scholar
[28]Zhang, Y.Z. and Gould, M.D., ‘Unitarity and complete reducibility of certain modules over quantized affine Lie algebras’, J. Math. Phys. 34 (1993), 6045–6059.Google Scholar