Published online by Cambridge University Press: 12 November 2018
Let 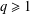 $q\geq 1$ be any integer and let
$q\geq 1$ be any integer and let 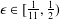 $\unicode[STIX]{x1D716}\in [\frac{1}{11},\frac{1}{2})$ be a given real number. We prove that for all primes
$\unicode[STIX]{x1D716}\in [\frac{1}{11},\frac{1}{2})$ be a given real number. We prove that for all primes 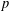 $p$ satisfying there exists a quadratic nonresidue
$p$ satisfying there exists a quadratic nonresidue 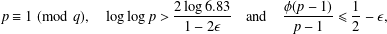 $$\begin{eqnarray}p\equiv 1\!\!\!\!\hspace{0.6em}({\rm mod}\hspace{0.2em}q),\quad \log \log p>\frac{2\log 6.83}{1-2\unicode[STIX]{x1D716}}\quad \text{and}\quad \frac{\unicode[STIX]{x1D719}(p-1)}{p-1}\leq \frac{1}{2}-\unicode[STIX]{x1D716},\end{eqnarray}$$
$$\begin{eqnarray}p\equiv 1\!\!\!\!\hspace{0.6em}({\rm mod}\hspace{0.2em}q),\quad \log \log p>\frac{2\log 6.83}{1-2\unicode[STIX]{x1D716}}\quad \text{and}\quad \frac{\unicode[STIX]{x1D719}(p-1)}{p-1}\leq \frac{1}{2}-\unicode[STIX]{x1D716},\end{eqnarray}$$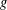 $g$ which is not a primitive root modulo
$g$ which is not a primitive root modulo 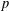 $p$ such that
$p$ such that 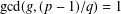 $\text{gcd}(g,(p-1)/q)=1$.
$\text{gcd}(g,(p-1)/q)=1$.