Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-08T16:11:29.757Z Has data issue: false hasContentIssue false
  • English
  • Français

PROPERTY L AND COMMUTING EXPONENTIALS IN DIMENSION AT MOST THREE

Part of: Basic linear algebra

Published online by Cambridge University Press:  28 June 2013

GERALD BOURGEOIS
GERALD BOURGEOIS*
Affiliation:
GAATI, Université de la Polynésie Française, BP 6570, 98702 FAA’A, Tahiti, Polynésie Française email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 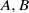$A, B$ be two square complex matrices of the same dimension 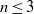$n\leq 3$. We show that the following conditions are equivalent. (i) There exists a finite subset 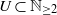$U\subset { \mathbb{N} }_{\geq 2} $ such that for every 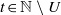$t\in \mathbb{N} \setminus U$, 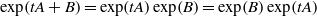$\exp (tA+ B)= \exp (tA)\exp (B)= \exp (B)\exp (tA)$. (ii) The pair 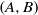$(A, B)$ has property L of Motzkin and Taussky and 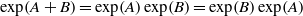$\exp (A+ B)= \exp (A)\exp (B)= \exp (B)\exp (A)$. We also characterise the pairs of real matrices 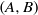$(A, B)$ of dimension three, that satisfy the previous conditions.

Keywords

matrix exponentialmatrix pencilproperty L

MSC classification

Secondary: 15A16: Matrix exponential and similar functions of matrices 15A22: Matrix pencils 15A24: Matrix equations and identities
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 70 - 78
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Baribeau, L. and Roy, S., ‘Caractérisation spectrale de la forme de Jordan’, Linear Algebra Appl. 320 (2000), 183–191.Google Scholar
Bourgeois, G., ‘On commuting exponentials in low dimensions’, Linear Algebra Appl. 423 (2007), 277–286.Google Scholar
Higham, N. J., Functions of Matrices: Theory and Computation (SIAM, Philadelphia, PA, 2008).CrossRefGoogle Scholar
Hille, E., ‘On roots and logarithms of elements of a complex Banach algebra’, Math. Ann. 136 (1958), 46–57.Google Scholar
Horn, R. and Piepmeyer, G., ‘Two applications of the theory of primary matrix functions’, Linear Algebra Appl. 361 (2003), 99–106.CrossRefGoogle Scholar
Morinaga, K. and Nôno, T., ‘On the non-commutative solutions of the exponential equation ${e}^{x} {e}^{y} = {e}^{x+ y} $’, J. Sci. Hiroshima Univ. Ser. A 17 (1954), 345–358.Google Scholar
Morinaga, K. and Nôno, T., ‘On the non-commutative solutions of the exponential equation ${e}^{x} {e}^{y} = {e}^{x+ y} $, II’, J. Sci. Hiroshima Univ. Ser. A 18 (1954), 137–178.Google Scholar
Motzkin, T. S. and Taussky, O., ‘Pairs of matrices with property L’, Trans. Amer. Math. Soc. 73 (1952), 108–114.Google Scholar
Schmoeger, Ch., ‘Remarks on commuting exponentials in Banach algebras. II’, Proc. Amer. Math. Soc. 128 (11) (2000), 3405–3409.CrossRefGoogle Scholar
de Seguins Pazzis, C., ‘On commuting matrices and exponentials’, Proc. Amer. Math. Soc. 141 (2013), 763–774.Google Scholar
Wermuth, E. M. E., ‘Two remarks on matrix exponentials’, Linear Algebra Appl. 117 (1989), 127–132.Google Scholar