Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T02:47:03.014Z Has data issue: false hasContentIssue false
  • English
  • Français

PROGRESS ON THE AUSLANDER–REITEN CONJECTURE

Part of: Representation theory of rings and algebras Local rings and semilocal rings Commutative algebra: Homological methods

Published online by Cambridge University Press:  16 March 2016

ABDOLNASER BAHLEKEH  and
ALI MAHIN FALLAH
ABDOLNASER BAHLEKEH*
Affiliation:
Department of Mathematics, Gonbade-Kavous University, 4971799151, Gonbade-Kavous, Iran email [email protected]
ALI MAHIN FALLAH
Affiliation:
Department of Mathematics, University of Isfahan, PO Box 81746-73441, Isfahan, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 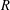$R$ be a commutative Gorenstein ring. A result of Araya reduces the Auslander–Reiten conjecture on the vanishing of self-extensions to the case where 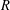$R$ has Krull dimension at most one. In this paper we extend Araya’s result to certain 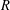$R$-algebras. As a consequence of our argument, we obtain examples of bound quiver algebras that satisfy the Auslander–Reiten conjecture.

Keywords

Gorenstein ringAuslander–Reiten conjectureGorenstein projective modules

MSC classification

Primary: 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.)
Secondary: 16G30: Representations of orders, lattices, algebras over commutative rings 13D02: Syzygies, resolutions, complexes 13D07: Homological functors on modules (Tor, Ext, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 3 , June 2016 , pp. 433 - 440
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Araya, T., ‘The Auslander–Reiten conjecture for Gorenstein rings’, Proc. Amer. Math. Soc. 137(6) (2009), 1941–1944.Google Scholar
Assem, I., Simson, D. and Skowronski, A., Elements of the Representation Theory of Associative Algebras (Cambridge University Press, Cambridge, 2006).Google Scholar
Auslander, M., ‘Functors and morphisms determined by objects’, in: Representation Theory of Algebras, Proc. Conf. Representation Theory, Philadelphia, 1967 (Marcel Dekker, New York, 1978), 1–244.Google Scholar
Auslander, M., ‘Isolated singularities and the existence of almost split sequences’, in: Proc. ICRA IV, Lecture Notes in Mathematics, 1178 (Springer, New York–Berlin, 1986), 194–241.Google Scholar
Auslander, M. and Bridger, M., Stable module theory, Memoirs of the American Mathematical Society, 94 (American Mathematical Society, Providence, RI, 1969).Google Scholar
Auslander, M., Ding, S. and Solberg, Ø., ‘Liftings and weak liftings of modules’, J. Algebra 158 (1993), 273–317.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., ‘On a generalized version of the Nakayama conjecture’, Proc. Amer. Math. Soc. 52 (1975), 69–74.Google Scholar
Bahlekeh, A., Dembegioti, F. and Talelli, O., ‘Gorenstein dimension and proper actions’, Bull. Lond. Math. Soc. 41(5) (2009), 859–871.CrossRefGoogle Scholar
Bahlekeh, A., Mahin Fallah, A. and Salarian, Sh., ‘On the Auslander–Reiten conjecture for algebras’, J. Algebra 427 (2015), 252–263.CrossRefGoogle Scholar
Celikbas, O. and Takahashi, R., ‘Auslander–Reiten conjecture and Auslander–Reiten duality’, J. Algebra 382 (2013), 100–114.Google Scholar
Christensen, L. W., Gorenstein Dimensions, Lecture Notes in Mathematics, 1747 (Springer, Berlin, 2000).CrossRefGoogle Scholar
Christensen, L. W. and Holm, H., ‘Algebras that satisfy Auslander’s condition on vanishing of cohomology’, Math. Z. 265 (2010), 21–40.CrossRefGoogle Scholar
Enochs, E. and Jenda, O. M. G., ‘Gorenstein injective and projective modules’, Math. Z. 220 (1995), 611–633.CrossRefGoogle Scholar
Enochs, E. and Jenda, O. M. G., Relative Homological Algebra (Walter de Gruyter, Berlin–New York, 2000).Google Scholar
Hoshino, M., ‘Modules without self-extensions and Nakayama’s conjecture’, Arch. Math. 43 (1984), 494–500.Google Scholar
Huneke, C. and Leuschke, G. J., ‘On a conjecture of Auslander and Reiten’, J. Algebra 275 (2004), 781–790.Google Scholar
Leuschke, G. J. and Wiegand, R., Cohen–Macaulay Representations, Mathematical Surveys and Monographs, 181 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Luo, R. and Huang, Z. Y., ‘When are torsionless modules projective?’, J. Algebra 320(5) (2008), 2156–2164.Google Scholar
Nakayama, T., ‘On algebras with complete homology’, Abh. Math. Semin. Univ. Hambg. 22 (1958), 300–307.Google Scholar
Sega, L. M., ‘Vanishing of cohomology over Gorenstein rings of small codimension’, Proc. Amer. Math. Soc. 131(8) (2003), 2313–2323.Google Scholar
Zhang, X., ‘A note on Gorenstein projective conjecture II’, Nanjing Daxue Xuebao Shuxue Bannian Kan 29(2) (2012), 155–162.Google Scholar