Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-11T04:36:54.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Power integral bases for real cyclotomic fields

Published online by Cambridge University Press:  17 April 2009

Laurel Miller-Sims  and
Leanne Robertson
Laurel Miller-Sims
Affiliation:
Department of Mathematics, Smith College, Northampton, MA 01063, United States of America, e-mail: [email protected], [email protected]
Leanne Robertson
Affiliation:
Department of Mathematics, Smith College, Northampton, MA 01063, United States of America, e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the problem of determining all power integral bases for the maximal real subfield Q (ζ + ζ−1) of the p-th cyclotomic field Q (ζ), where p ≥ 5 is prime and ζ is a primitive p-th root of unity. The ring of integers is Z[ζ+ζ−1] so a power integral basis always exists, and there are further non-obvious generators for the ring. Specifically, we prove that 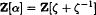if 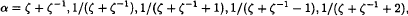or one of the Galois conjugates of these five algebraic integers. Up to integer translation and multiplication by −1, there are no additional generators for p ≤ 11, and it is plausible that there are no additional generators for p > 13 as well. For p = 13 there is an additional generator, but we show that it does not generalise to an additional generator for 13 < p < 1000.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 71 , Issue 1 , February 2005 , pp. 167 - 173
Copyright
Copyright © Australian Mathematical Society 2005

References

[1]Bremner, A., ‘On power bases in cyclotomic number fields’, J. Number Theory 28 (1988), 288–298.CrossRefGoogle Scholar
[2]Gaál, I., ‘Computing all power integral bases in orders of totally real cyclic sextic number fields’, Math. Comp. 65 (1996), 801–822.CrossRefGoogle Scholar
[3]Gaál, I., Diophantine equations and power integral bases. New computational methods (Birkhäuser, Boston, 2002).CrossRefGoogle Scholar
[4]Gaál, I. and Phost, M., ‘Power integral bases in a parametric family of totally real cyclic quintics’, Math. Comp. 66 (1997), 1689–1696.CrossRefGoogle Scholar
[5]Gaál, I. and Schulte, N., ‘Computing all power integral bases of cubic fields’, Math. Comp. 53 (1989), 689–696.CrossRefGoogle Scholar
[6]Gras, M.-N., ‘Non monogénéité de l'anneau des entiers des extensions cycliques de Q de degré premier l ≥ 5’, J. Number Theory 23 (1986), 347–353.CrossRefGoogle Scholar
[7]Győry, K., ‘Sur les polynômes à coefficients entiers et de discriminant donné, III’, Publ. Math. Debrecen 23 (1976), 141–165.CrossRefGoogle Scholar
[8]Miller-Sims, L., Power bases for real cyclotomic fields, (unpublished honors thesis, Smith College, 2003).Google Scholar
[9]Nagell, T., ‘Sur les discriminants des nombres algébriques’, Ark. Mat. 7 (1967), 265–282.CrossRefGoogle Scholar
[10]Robertson, L., ‘Power bases for cyclotomic integer rings’, J. Number Theory 69 (1998), 98–118.CrossRefGoogle Scholar
[11]Robertson, L., ‘Power bases for 2-power cyclotomic fields’, J. Number Theory 88 (2001), 196–209.CrossRefGoogle Scholar