Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T06:04:10.800Z Has data issue: false hasContentIssue false
  • English
  • Français

Positioning matrices with respect to the boundary of the maximal group

Published online by Cambridge University Press:  17 April 2009

J. DeFranza  and
D.J. Fleming
J. DeFranza
Affiliation:
Department of Mathematics, St. Lawrence University, Canton, NY 13617U.S.A.
D.J. Fleming
Affiliation:
Department of Mathematics, St. Lawrence University, Canton, NY 13617U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Δ denote the Banach algebra of all conservative triangular matrics, M the maximal group of invertible elements of Δ, B the boundary of M and 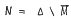. In this note little Nörlund means are located with respect to the disjoint decomposition M u B u N of Δ in terms of the zeros of the generating power series. Further, corridor matrices of finite type, that is, conservative methods with finitely many convergent diagonals, are located with respect to M u B u N.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 33 , Issue 1 , February 1986 , pp. 113 - 122
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Berg, I.D., “Open Sets of Conservative Matrices”, Proc. Amer. Math. Soc. 16 (1965) 719–724.CrossRefGoogle Scholar
[2]Borwein, D. and Thorpe, B., “Conditions for Inclusion Between Nörlund Summability Methods”. (preprint)Google Scholar
[3]Copping, J., “Mercerian Theorems and Inverse Transforms”, Studia Math., 21 (1962) 177–194.CrossRefGoogle Scholar
[4]DeFranza, J. and Fleming, D.J., “The Banach Algebra of Conservative Triangular Matrices”, Math. Z. 180 (1982), 463–468.CrossRefGoogle Scholar
[5]DeFranza, J. and Fleming, D.J., “Nörlund Polynomial Methods of Type M(E)”, Houston J. Math, 10 (1984).Google Scholar
[6]Erdos, P. and Piranian, G., “Laconicity and Redundancy of Toeplitz Matrices”, Math. Z. 83 (1964) 381–394.CrossRefGoogle Scholar
[7]Hill, J.D., “On Perfect Methods of Summability”, Duke Math. J. 3 (1937) 702–714.CrossRefGoogle Scholar
[8]Mazur, S., “Line Anwendung der Theorie der Operationen bei Untersuchung der Toeplitzschen Limitierungsrerfahrem,” Studia Math. 2 (1930) 40–50.CrossRefGoogle Scholar
[9]Ramanujan, M.S., “On Summability Methods od Type M”, J. London Math. Soc. 29 (1954) 184–189.CrossRefGoogle Scholar
[10]Rhoades, B.E., “Triangular Summability Methods and the Boundary of the Maximal Group”, Math. Z. 105 (1968), 284–290.CrossRefGoogle Scholar
[11]Rudin, W., Functional Analysis, (McGraw-Hill Co., 1973).Google Scholar
[12]Sharma, N.K., “Spectra of Conservative Matrices”, Proc. Amer. Math. Soc., 35 (1972) 515–518.CrossRefGoogle Scholar
[13]Sharma, N.K., “Nörlund Methods Associated with Analytic Functions”, Iran. J. Sci. & Tech. 3 (1975) 285–289.Google Scholar
[14]Silvermann, H., Complex Variables, (Houghton-Mifflin Co., 1975).Google Scholar
[15]Zygmund, A., Trigonometric Series, (Cambridge, 1959).Google Scholar