Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T02:58:21.267Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomials and functions with finite spectra on locally compact Abelian groups

Published online by Cambridge University Press:  17 April 2009

B. Basit  and
A.J. Pryde
B. Basit
Affiliation:
Department of MathematicsMonash UniversityClayton Vic 3168Australia E-mail: [email protected]@vaxc.cc.monash.edu.au
A.J. Pryde
Affiliation:
Department of MathematicsMonash UniversityClayton Vic 3168Australia E-mail: [email protected]@vaxc.cc.monash.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we define polynomials on a locally compact Abelian group G and prove the equivalence of our definition with that of Domar. We explore the properties of polynomials and determine their spectra. We also characterise the primary ideals of certain Beurling algebras 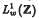on the group of integers Z. This allows us to classify those elements of 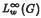that have finite spectrum. If ϕ is a uniformly continuous function with bounded differences then there is a Beurling algebra naturally associated with ϕ. We give a condition on the spectrum of ϕ relative to this algebra which ensures that ϕ is bounded. Finally we give spectral conditions on a bounded function on ℝ that ensure that its indefinite integral is bounded.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 51 , Issue 1 , February 1995 , pp. 33 - 42
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Domar, Y., ‘Harmonic analysis based on certain Banach algebras’, Acta Math. 96 (1956), 1–66.CrossRefGoogle Scholar
[2]Dunford, N. and Schwartz, J.T., Linear operators, Part II (Interscience Publishers, New York, London, 1963).Google Scholar
[3]Loomis, L.H., An introduction to harmonic nalysis (D. Van Nostrand Comp., Inc., 1953).Google Scholar
[4]Naimark, M.A., Normed rings, (translated from Russian) (P. Noordhoff, N.y. Groningen, The Netherlands, 1959).Google Scholar
[5]Reiter, H., Classical harmonic analysis and locally compact groups, Oxford Math. Monographs (Oxford University, 1968).Google Scholar
[6]Rudin, W., Fourier analysis on groups (Interscience, New York, London, 1962).Google Scholar